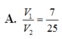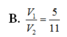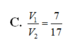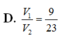Chọn C
Gọi V1, V2 lần lượt là thể tích hình chóp và thể tích khối hộp (hình vẽ).
Khi đó 
(S, h lần lượt là diện tích đáy và chiều cao của khối hộp
Cho hình chóp S.ABCD có đáy là hình vuông, SA vuông góc với đáy, SA = AC. Mặt phẳng qua A vuông góc với SC cắt SB, SC, SD lần lượt tại B', C', D'. Tỉ số giữa thể tích hình chóp S.A'B'C'D' và thể tích hình chóp S.ABCD là:
A. 1/6 B. 1/4
C. 1/3 D. 1/2
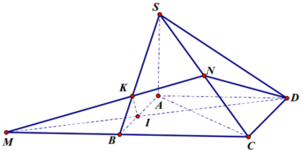
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, B A D ^ = 60 ° và SA vuông góc với mặt phẳng (ABCD). Góc giữa 2 mặt phẳng (SBD) và (ABCD) bằng 450. Gọi M là điểm đối xứng của C qua B và N là trung điểm của SC. Mặt phẳng (MND) chia khối chóp S.ABCD thành hai khối đa diện, trong đó khối đa diện chứa đỉnh S có thể tích V1, khối đa diện còn lại có thể tích V2 (tham khảo hình vẽ bên). Tính tỉ số V 1 V 2
A. V 1 V 2 = 12 7
B. V 1 V 2 = 5 3
C. V 1 V 2 = 1 5
D. V 1 V 2 = 7 5
Cho mặt cầu (S) tâm O, bán kính bằng 2. (P) là mặt phẳng cách O một khoảng bằng 1 và cắt (S) theo một đường tròn (C). Hình nón (N) có đáy là (C), đỉnh thuộc (S), đỉnh cách (P) một khoảng lớn hơn 2. Kí hiệu V 1 , V 2 lần lượt là thể tích của khối cầu (S) và khối nón (N). Tỉ số V 1 V 2 là
Cho khối chóp S.ABCD có đáy là hình bình bành thể tích bằng 1. Gọi M là điểm đối xứng của C qua B;N là trung điểm cạnh SC. Mặt phẳng (MDN) chia khối chóp S.ABCD thành hai khối đa diện, thể tích của khối đa diện chứa đỉnh S bằng
A. 5 6
B. 5 8
C. 12 19
D. 7 12
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, B A D ^ = 60 ° và SA vuông góc với mặt phẳng (ABCD). Góc giữa hai mặt phẳng (SBD) và (ABCD) bằng 45 ° . Gọi M là điểm đối xứng của C qua B và N là trung điểm của SC. Mặt phẳng (MND) chia khối chóp S.ABCD thành hai khối đa diện, trong đó khối đa diện chứa đỉnh S có thể tích V 1 , khối đa diện còn lại có thể tích V 2 (tham khảo hình vẽ bên).
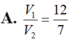
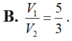
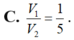
Cho khối hộp H có thể tích V. Xét tất cả các khối chóp tứ giác có đỉnh của chóp và các đỉnh của mặt đáy đều là đỉnh của H. Chọn câu đúng.
A. Tất cả các khối chóp đó có thể tích bằng V 3
B. Tất cả các khối chóp đó có thể tích bằng V 6
C. Có khối chóp có thể tích bằng V 3 , có khối chóp có thể tích bằng V 6
D. Không có khối chóp có thể tích bằng V 3 , không có khối chóp có thể tích bằng V 6
Cho khối hộp ABCD. A'B'C'D' có đáy là hình chữ nhật với AB = 3 ; AD = 7 . Hai mặt bên (ABB'A') và (ADD'A') cùng tạo với đáy góc 450, cạnh bên của hình hộp bằng 1 (hình vẽ). Thể tích khối hộp là:
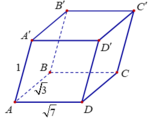
A. 7
B. 3 3
C. 5
D. 7 7
Cho khối chóp tứ giác đều S.ABCD. Gọi M là trung điểm SC, mặt phẳng (P) chứa AM và song song với BD chia khối chóp thành 2 khối đa diện. Đặt V 1 là thể tích khối đa diện có chứa đỉnh S và V 2 là thể tích khối đa diện có chứa đáy. Tỉ số V 1 V 2 bằng:
A. V 1 V 2 = 3 2
B. V 1 V 2 = 1 2
C. V 1 V 2 = 2 3
D. V 1 V 2 = 1
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi K,M lần lượt là trung điểm của các đoạn thẳng SA, SB, α là mặt phẳng qua K song song với AC và AM. Mặt phẳng α chia khối chóp S.ABCD thành hai khối đa diện. Gọi V1 là thể tích của khối đa diện chứa đỉnh S và V2 là thể tích khối đa diện còn lại. Tính tỉ số V 1 V 2 .
