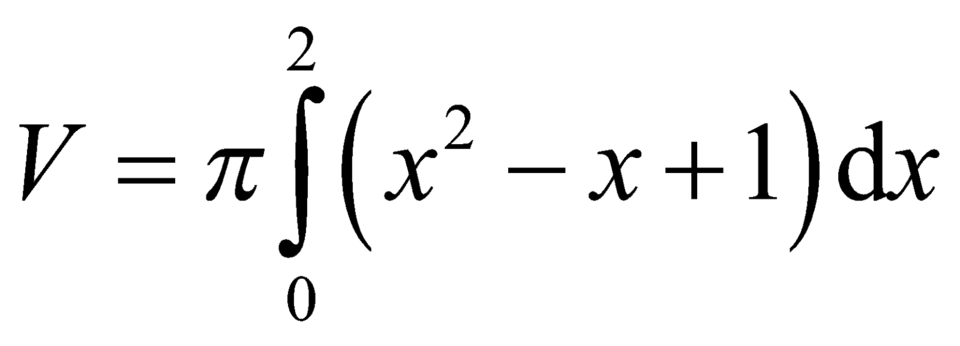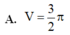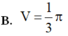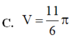Các câu hỏi tương tự
Thể tích vật thể tròn xoay khi quay hình phẳng giới hạn bởi các đường
y
ln
x
,
y
0
,
x
2
quanh trục Ox là:
Đọc tiếp
Thể tích vật thể tròn xoay khi quay hình phẳng giới hạn bởi các đường y = ln x , y = 0 , x = 2 quanh trục Ox là:
![]()
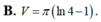
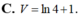
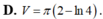
Cho hình phẳng giới hạn bởi các đường
y
tan
x
;
y
0
;
x
0
;
x
π
4
quay xung quanh trục Ox. Tính thể tích vật thể tròn xoay được sinh ra.
Đọc tiếp
Cho hình phẳng giới hạn bởi các đường y = tan x ; y = 0 ; x = 0 ; x = π 4 quay xung quanh trục Ox. Tính thể tích vật thể tròn xoay được sinh ra.
![]()
![]()
![]()
![]()
Cho hình phẳng (H) giới hạn bởi các đường
y
e
x
,
y
0
,
x
0
,
x
k
k
0
. Gọi
V
k
là thể tích khối tròn xoay khi quay hình (H) quanh trục Ox. Biết rằng
V
k
4
π...
Đọc tiếp
Cho hình phẳng (H) giới hạn bởi các đường y = e x , y = 0 , x = 0 , x = k k > 0 . Gọi V k là thể tích khối tròn xoay khi quay hình (H) quanh trục Ox. Biết rằng V k = 4 π . Kết luận nào sau đây là đúng?
A. 1 < k < 3 2 .
B. 3 2 < k < 2.
C. 1 2 < k < 1.
D. 0 < k < 1 2 .
Tính thể tích vật thể tròn xoay quanh trục Ox sinh bởi hình phẳng giới hạn bởi các đường y 0,
y
cos
6
x
+
sin
6
x
, x 0,
x
π
2
A.
-
11
π
2
16
B.
11...
Đọc tiếp
Tính thể tích vật thể tròn xoay quanh trục Ox sinh bởi hình phẳng giới hạn bởi các đường y = 0, y = cos 6 x + sin 6 x , x = 0, x = π 2
A. - 11 π 2 16
B. 11 π 2 16
C. π 2 8
D. 5 π 2 16
Tính thể tích của vật thể tròn xoay khi quay các hình phẳng giới hạn bởi các đường sau quanh trục Ox: y = 2x/ π ; y = sinx; x ∈ [0; π /2]
Tính thể tích của vật thể tròn xoay khi quay các hình phẳng giới hạn bởi các đường sau quanh trục Ox: y = x α , α ∈ N*; y = 0; x = 0
Thể tích khối tròn xoay sinh ra bởi hình phẳng giới hạn bởi các đường
y
1
x
-
3
, y 0; x 0; x 2 quay một vòng quanh trục Ox là A.
2
π
B.
2
π
3
C.
4
π
3...
Đọc tiếp
Thể tích khối tròn xoay sinh ra bởi hình phẳng giới hạn bởi các đường y = 1 x - 3 , y = 0; x = 0; x= 2 quay một vòng quanh trục Ox là
A. 2 π
B. 2 π 3
C. 4 π 3
D. π 3
Thể tích vật thể tròn xoay khi cho hình phẳng (H) giới hạn bởi các đường
y
x
ln
x
y
0
;
x
2
quay quanh trục Ox được tính bởi công thức nào?
Đọc tiếp
Thể tích vật thể tròn xoay khi cho hình phẳng (H) giới hạn bởi các đường y = x ln x y = 0 ; x = 2 quay quanh trục Ox được tính bởi công thức nào?
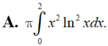
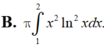
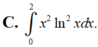
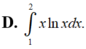
Cho hình phẳng (H) giới hạn bởi các đường
y
x
2
-
x
+
1
, y0, x0, x2. Gọi V là thể tích khối tròn xoay được tạo thành khi quay (H) xung quanh trục Ox. Mệnh đề nào sau đây đúng? A. B. C. D.
Đọc tiếp
Cho hình phẳng (H) giới hạn bởi các đường y = x 2 - x + 1 , y=0, x=0, x=2. Gọi V là thể tích khối tròn xoay được tạo thành khi quay (H) xung quanh trục Ox. Mệnh đề nào sau đây đúng?
A. 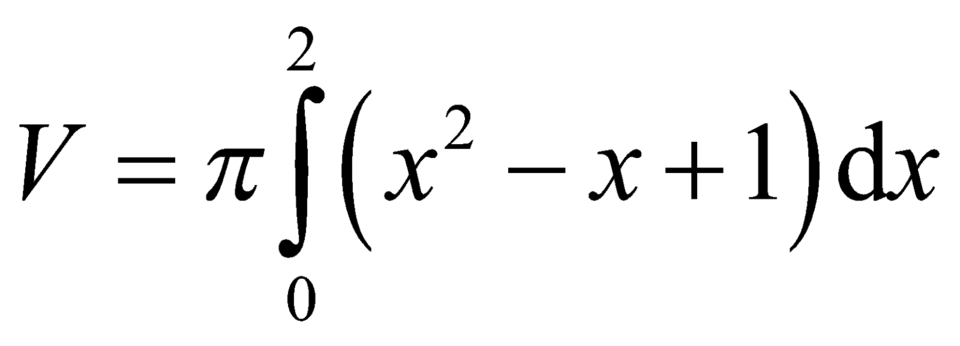
B. 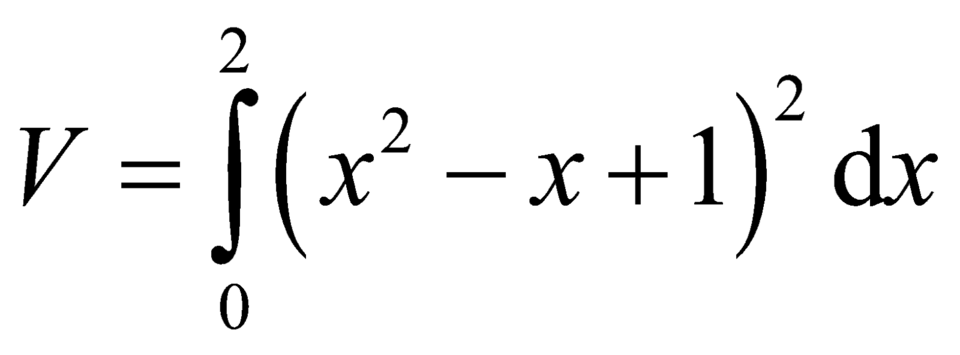
C. 
D.