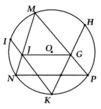
KG là đường phân giác của M K P ^ => M G G P = M K K P (1)
KJ là đường phân giác của M K N ^ => M J J N = M K K N (2)
Chứng minh được: KN = KP (3)
Từ (1); (2); (3) => M G G P = M J J N => Đpcm

KG là đường phân giác của M K P ^ => M G G P = M K K P (1)
KJ là đường phân giác của M K N ^ => M J J N = M K K N (2)
Chứng minh được: KN = KP (3)
Từ (1); (2); (3) => M G G P = M J J N => Đpcm
Tam giác ABC nội tiếp đường tròn tâm O, các điểm M, N, P là điểm chính giữa của các cung AB, BC, CA. Gọi D là giao điểm của MN và AB, E là giao điểm của PN và AC. Chứng minh rằng DE song song với BC.
Tam giác ABC nội tiếp đường tròn tâm O, các điểm M, N, P là điểm chính giữa của các cung AB, BC, CA. Gọi D là giao điểm của MN và AB, E là giao điểm của PN và AC. Chứng minh rằng DE song song với BC.
Tam giác ABC nội tiếp đường tròn tâm O, các điểm M, N, P là điểm chính giữa của các cung AB, BC, CA. Gọi D là giao điểm của MN và AB, E là giao điểm của PN và AC. Chứng minh rằng DE song song với BC.
Cho đường tròn (O) và điểm M nằm ngoài (O). Từ M kẻ hai tiếp tuyến MA, MB đển (O) (A, B là các tiếp điểm). Qua M kẻ cát tuyên MNP (MN < MP) đến (O). Gọi K là trung điểm của NP
a, Cho đường tròn (O) và điểm M nằm ngoài (O). Từ M kẻ hai
b, Chứng minh tia KM là phân giác của góc A K B ^
c, Gọi Q là giao điểm thứ hai của BK với (O). Chứng minh AQ song song NP
d, Gọi H là giao điểm của AB và MO. Chứng minh: MA2 = MH.MO = MN.MP
e, Chứng minh bốn điểm N, H, O, P cùng thuộc một đường tròn
Cho tam giác MNP có 3 góc nhọn , MN < MP . Gọi I là trung điểm của NP , H,K lần lượt là chân đường cao của tam giác MNP kẻ từ N và P; O là trực tâm. L là giao điểm của HK và NP. Chứng minh : LO vuông góc với MI.
Cho đường tròn (O). Từ điểm M cố định nằm ngoài đường tròn, kẻ các cát tuyến MNP
(N nằm giữa M và P) và hai tiếp tuyến MA, MB với đường tròn (A, B là tiếp điểm, A thuộc
nửa mặt phẳng bờ MP chứa điểm O) với đường tròn (O). Gọi I là trung điểm của NP.
a) Chứng minh tứ giác MOIB nội tiếp đường tròn.
b) Chứng minh MB2 = MN. MP
c) Gọi C là giao điểm của BI với đường tròn tâm O. Chứng minh AC // MP
d) Gọi H là giao điểm của MO và AB. Khi cát tuyến MNP thay đổi thì trọng tâm tầm giác ANP chạy trên đường nào?
cho nửa đường tròn tâm O đường kính MN=5cm. Trên nửa đường tròn lấy điểm P sao cho MP=3.Vẽ PH vuông góc với MN H thuộc MN
a) cm: tam giác MNP vuông từ đó tính MH,PH, goc MNP
b) qua O vẽ đường thẳng song song với NP cắt tiếp tuyến tại M của nửa đường tròn tại I.
CM: IP là tiếp tuyến của đường tròn (O)
c) gọi K là giao điểm của NI và PH. Chứng minh K là trung điểm PH
Cho tam giác ABC nội tiếp đường tròn ( O ), các điểm M , N , P là các điểm chính giữa của cac cung AB , BC và Ac . Gọi D là giao điểm của MN và Ab , E là giao điểm của PN và AC . Chứng minh : DE song song BC .
Cho tam giác đều MNP nội tiếp đường tròn tâm (O). Điểm D di chuyển trên M P ⏜ . Gọi E là giao điểm của MP và ND, gọi F là giao điểm của MD và NP. Chứng minh: M F N ^ = M N D ^