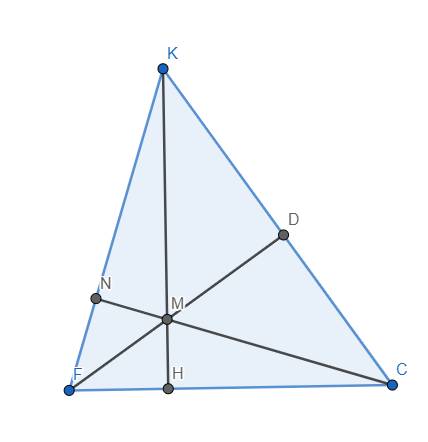
Dễ thấy \(\widehat{HKF}=\widehat{HCM}\) (cùng phụ với \(\widehat{ABC}\))
Xét tam giác HKF và HCM, có: \(\widehat{KHF}=\widehat{CHM}\left(=90^o\right)\) và \(\widehat{HKF}=\widehat{HCM}\) (cmt)
Suy ra \(\Delta HKF~\Delta HCM\left(g.g\right)\)
\(\Rightarrow\dfrac{HK}{HC}=\dfrac{HF}{HM}\) \(\Rightarrow HK.HM=HC.HF\)
Mà \(HC.HF\le\dfrac{\left(HC+HF\right)^2}{4}=\dfrac{FC^2}{4}\) (BĐT Cô-si), suy ra \(HK.HM\le\dfrac{FC^2}{4}\) (đpcm)
Dấu "=" xảy ra \(\Leftrightarrow HC=HF\) \(\Leftrightarrow\) H là trung điểm CF \(\Leftrightarrow\Delta KFC\) cân tại K.











