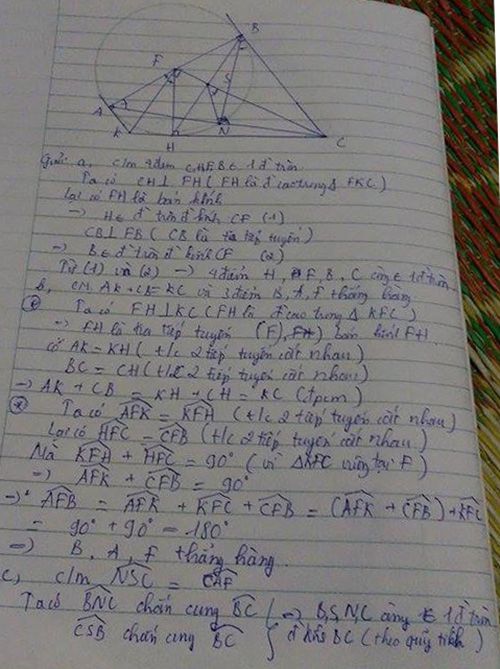 CÓ PHẢI KO
CÓ PHẢI KO
KO PHẢI THÌ THÔI NHÉ
Hệ thức lượng:
\(\Delta FEG\left(\widehat{F}=90^o\right)\) có:
\(\frac{1}{FH^2}=\frac{1}{FG^2}+\frac{1}{FI^2}\Leftrightarrow\frac{1}{FH^2}=\frac{1}{16^2}+\frac{1}{12^2}\Leftrightarrow FH=9,6\)
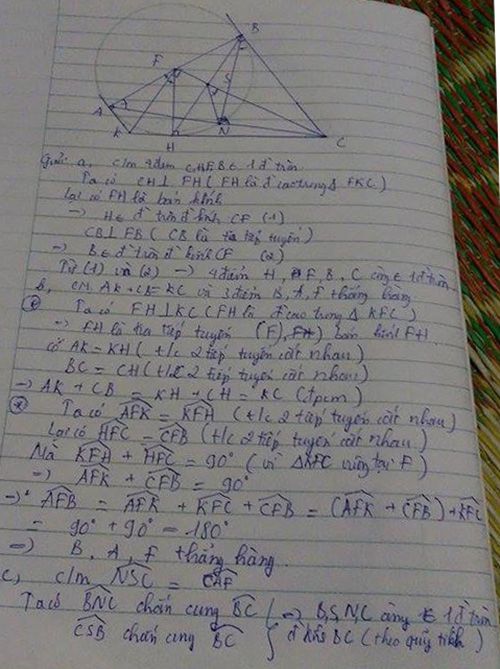 CÓ PHẢI KO
CÓ PHẢI KO
KO PHẢI THÌ THÔI NHÉ
Hệ thức lượng:
\(\Delta FEG\left(\widehat{F}=90^o\right)\) có:
\(\frac{1}{FH^2}=\frac{1}{FG^2}+\frac{1}{FI^2}\Leftrightarrow\frac{1}{FH^2}=\frac{1}{16^2}+\frac{1}{12^2}\Leftrightarrow FH=9,6\)
cho tam giác ABC đường cao AH kẻ HE vuông góc với AB tại E, HE vuông góc với AC tại F trên tia đối của EH,FH lấy M,N sao cho EH=EM FH=FN
tìm điều kiện của tam giác ABC để BM và CN song song
Cho hình tam giác ABC có BAC bằng 50 độ,ABC bằng 70 độ.Gọi BE là tia phân giác của ABC (e thuộc AC).Từ E kẻ EF//AB(F thuộc BC).Từ F kẻ tia phân giác FH của EFC(H thuộc BC).
a,Tính BEF và CEF
b,Qua F kẻ đường thẳng d vuông góc với BE cắt AB tại K.Tính BFK
Cho tam giác ABC cân tại A , đường cao AH , E là hình chiếu của H xuống AB , F là hình chiếu của H xuống AC . Trên tia đối tia EH lấy M sao cho EH = EM . Trên tia đối tia FH lấy N sao cho FH = FN .
CMR : tam giác AMN cân .
Cho tam giác ABC vuông tại A. Đường trung trực của AB cắt AB tại E và BC tại F
a) CM FA=FB
b) Từ F vẽ FH vuông góc với AC. CM FH vuông gốc với EF
c) Cm FH= AE
d) CM EH= BC/2 và EH//BC
Cho tam giác ABD có góc B=2 góc D. Kẻ đường cao AH trên tia đối của tia BA lấy BE= BH.Đường thăng EH cắt AD tại F chắng minh FH=FD,FA=FH
Bai 1 cho tam giác ABC vuông tại A có góc C=30 độ đường cao AH Trên đoạn HC lấy điểm D sao cho HD=HB Từ C kẻ CE vuông góc AD chứng minh
a) Tam giác ABD là tam giác đều
b) AH = CE
Bài 2 cho tam giác ABC ( góc A = 90 độ) đường trung trực của AB cắt AB tại E và cắt BC tại G
a) chưngs minh DA=DB
b) tư F vẽ DH vuông góc AC(H thuộc AC) CM FH vuông góc EF
c)Chưngs minh FH=AE
Cho tam giác vuông ABC có góc A bằng 90 độ. Đường trung trực của AB cắt AB tại E và BC tại F
a. Chứng minh FA = FB
b. Từ F vẽ FH vuông góc với AC ( H thuộc AC ) . Chứng minh FH vuông góc È
c. Chứng minh FH = AE
d. Chứng minh EH // BC và EH = BC/2
Cho tam giác ABC vuông tại A. Đường trung trực của AB cắt AB tại E và BC tại F.
a) Chứng minh FA = FB
b) Từ F vẽ FH vuông góc với AC (H thuộc AC. Chứng minh FH vuông góc với EF
c) Chứng minh FH = AE
d) Chứng minh EH = BC/2 và EH // BC