Question

Số tiếp tuyến đi qua điểm A(1;-6) của đồ thị hàm số y = x 3 - 3 x + 1  là:

A. 0

B. 2

C. 1

D. 3

Answer 1

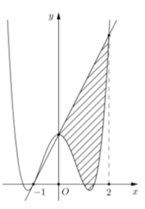
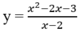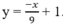Chọn C

Phương pháp:

Cho hàm số y = f(x) và M( x 0 ; y 0 )

Bước 1: Gọi ( ∆ ) là tiếp tuyến của đồ thị hàm số đã cho của đồ thị hàm số y = f(x); ( ∆ ) đi qua M( x 0 ; y 0 ) và có hệ số góc k.

Bước 2: ( ∆ ) có dạng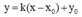 

Để ( ∆ ) tiếp xúc với đồ thị y = f(x) thì hệ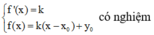 

Bước 3: Giải hệ bằng phương pháp thế, số nghiệm của hệ là số tiếp tuyến ( ∆ ) tìm được.

 

Cách giải:

Gọi k là hệ số góc tiếp tuyến ( ∆ ) với đồ thị (C) đi qua A(1;-6)

=>( ∆ ) có dạng: y = k(x-1) - 6

Để ( ∆ )  tiếp xúc với (C) thì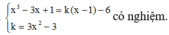  

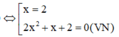
Vậy có 1 pttt đi qua A(1;-6).