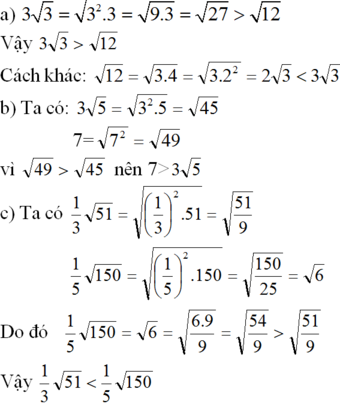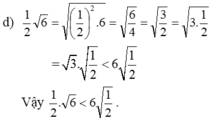Các câu hỏi tương tự
So sánh :
a,\(\frac{7}{23}v\text{à}\frac{11}{28}\)
b,\(\frac{2014}{2015}+\frac{2015}{2016}v\text{à}\frac{2014+2015}{2015+2016}\)
c,A=\(\frac{2^{10}+1}{2^{11}+1}v\text{à B=\frac{2^{11}+1}{2^{12}+1}}\)
Không dùng máy tính ,hãy so sánh :
1 )\(\sqrt{7-\sqrt{21}+4\sqrt{5}}v\text{à}\sqrt{5}-1\)
2 )\(\sqrt{5}+\sqrt{10}+1v\text{à}\sqrt{35}.\)
3 )\(\frac{15-2\sqrt{10}}{3}v\text{à}\sqrt{15}.\)
so sánh\(\sqrt[3]{\left(1-\sqrt{3}\right)\left(4-2\sqrt{3}\right)}v\text{à}\sqrt[3]{\left(1-\sqrt{5}\right)\left(6-2\sqrt{5}\right)}\)
so sánh: a/ 4 và\(1+2\sqrt{2}\) b/4 và\(2\sqrt{6}-1\) c/\(-3\sqrt{3}v\text{à}-2\sqrt{7}\)
So Sánh Các Biểu Thức Sau:
a,\(\sqrt{2}+\sqrt{11}v\text{à}\sqrt{3}+4\) 4
b, \(\sqrt{21}-\sqrt{5}v\text{à}\)\(\sqrt{20}-\sqrt{6}\)
c,\(\sqrt{24}-1v\text{à}\)\(5\)
So sánh
a) 3√3 và √12
b) 7 và 3√5
c) 1/3√51 và 1/5√150
d) 1/2√6 và 6√1/2
12+3+5+6889+1=
anh đây chỉ thích hot girl thôi à
Ttext{ìm} stext{ố}.nguytext{ê}n.dtext{ư}text{ơ}ng.nhtext{ỏ}.nhtext{ất}.thtext{ỏa}.mtext{ãn}:frac{1}{2}stext{ố}.text{đ}text{ó}.ltext{à}.stext{ố}.chtext{ính}.phtext{ư}text{ơ}ng frac{1}{3}stext{ố}.text{đ}text{ó}.ltext{à}.ltext{ập}.phtext{ư}text{ơ}ng.ctext{ủa}.1.stext{ố}.nguytext{ên} frac{1}{5}stext{ố}.text{đ}text{ó}.ltext{à}.ltext{ũy}.thtext{ừa}.5.ctext{ủa}.1.stext{ố.nguytext{ê}n}
Đọc tiếp
\(T\text{ìm}\) \(s\text{ố}.nguy\text{ê}n.d\text{ư}\text{ơ}ng.nh\text{ỏ}.nh\text{ất}.th\text{ỏa}.m\text{ãn}:\frac{1}{2}s\text{ố}.\text{đ}\text{ó}.l\text{à}.s\text{ố}.ch\text{ính}.ph\text{ư}\text{ơ}ng\) \(\frac{1}{3}s\text{ố}.\text{đ}\text{ó}.l\text{à}.l\text{ập}.ph\text{ư}\text{ơ}ng.c\text{ủa}.1.s\text{ố}.nguy\text{ên}\) \(\)
\(\frac{1}{5}s\text{ố}.\text{đ}\text{ó}.l\text{à}.l\text{ũy}.th\text{ừa}.5.c\text{ủa}.1.s\text{ố.nguy\text{ê}n}\)
So sánh
\(\sqrt{2012}+\sqrt{2013}+\sqrt{2014}v\text{à}\sqrt{2009}+\sqrt{2011}+\sqrt{2019}\)
\(Cho\)\(a,b,c\in R^+\)\(v\text{à}\)\(abc=\frac{1}{6}\)
Chứng minh rằng \(3+\frac{a}{2b}+\frac{2b}{3c}+\frac{3c}{a}\ge a+2b+3c+\frac{1}{a}+\frac{1}{2b}+\frac{1}{3c}\)
Giúp mìk với