Các câu hỏi tương tự
Trên mặt phẳng tọa độ tìm tập hợp điểm biểu diễn các số phức z thỏa mãn điều kiện:
a) Phần thực của z bằng phần ảo của nó ;
b) Phần thực của z là số đối của phần ảo của nó ;
c) Phần ảo của z bằng hai lần phần thực của nó cộng với 1;
d) Modun của z bằng 1, phần thực của z không âm.
Cho số phức z thỏa mãn
5
z
+
i
2
-
i
z
+
1
. Gọ...
Đọc tiếp
Cho số phức z thỏa mãn 5 z + i = 2 - i z + 1 . Gọi a, b lần lượt là phần thực và phần ảo của số phức 1 + z + z 2 , tổng a+b bằng
A. 13
B. -5
C. 9
D. 5
Biết rằng hai số phức
z
1
,
z
2
thỏa mãn
|
z
1
-
3
-
4
i
|
1
và
|
z
2
-
3
-
4
i
|
1
2
. Số phức z có phần thực là a v...
Đọc tiếp
Biết rằng hai số phức z 1 , z 2 thỏa mãn | z 1 - 3 - 4 i | = 1 và | z 2 - 3 - 4 i | = 1 2 . Số phức z có phần thực là a và phần ảo là b thỏa mãn 3 a - 2 b = 12 . Giá trị nhỏ nhất của P = | z - z 1 | + | z - 2 z 2 | + 2 bằng:
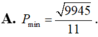
![]()
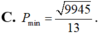
![]()
Gọi z là số phức có môđun nhỏ nhất và thỏa mãn
z
+
1
+
i
z
¯
+
i
. Tổng phần thực và phần ảo của số phức z bằng
Đọc tiếp
Gọi z là số phức có môđun nhỏ nhất và thỏa mãn z + 1 + i = z ¯ + i . Tổng phần thực và phần ảo của số phức z bằng
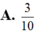
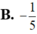
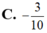
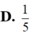
Cho số phức z cóphần thực bằng 2 và phần ảo bằng -3.Modul của số phức 3+iz là A.. B. . C. D..
Đọc tiếp
Cho số phức z cóphần thực bằng 2 và phần ảo bằng -3.Modul của số phức 3+iz là
A.![]() .
.
B. ![]() .
.
C. ![]()
D.![]() .
.
Viết số phức z có phần thực bằng 1/2, phần ảo bằng - 3 2 .
a) Cho hai số phức z1 = 1 + 2i ; z2 = 2 – 3i . Xác định phần thực và phần ảo của số phức z1 – 2z2 .
b) Cho hai số phức z1 = 2 + 5i ; z2 = 3 – 4i . Xác định phần thực và phần ảo của số phức z1.z2
Biết tập hợp điểm M biểu diễn số phức z là đường thẳng (d): 3x + 2y – 5 = 0. Tìm số phức z sao cho phần thực và phần ảo bằng nhau
A. z = 5 + 5i
B. z = 5 – 5i
C. z = -5 + 5i
D. z = 1 + i
Trong mặt phẳng phức với hệ tọa độ Oxyz, tập hợp điểm biểu diễn số phức z có phần thực bằng 3 lần phần ảo là
A. Đường elip
B. Đường tròn
C. Đường thẳng
D. Đường parabol



