Đáp án B
Giả sử ta có tứ diện đều ABCD, mặt phẳng đối xứng của tứ diện ABCD chính là các mặt phẳng trung trực ứng với từng cạnh của tứ diện ấy.
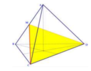
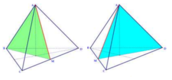
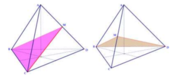
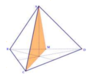
Đáp án B
Giả sử ta có tứ diện đều ABCD, mặt phẳng đối xứng của tứ diện ABCD chính là các mặt phẳng trung trực ứng với từng cạnh của tứ diện ấy.




Tứ diện đều có bao nhiêu mặt phẳng đối xứng?
A. 2
B. 3
C. 6
D. 9
Số mặt phẳng đối xứng của khối tứ diện đều là
A. 6
B. 7
C. 9
D. 9
Hình chóp tứ giác đều có bao nhiêu mặt phẳng đối xứng?
A. 1
B. 2
C. 3
D. 4
Trên mặt phẳng (α) cho hình vuông ABCD. Các tia Ax, By, Cz, Dt vuông góc với mặt phẳng (α) và nằm về một phía đối với mặt phẳng (α). Một mặt phẳng (β) lần lượt cắt Ax, By, Cz, Dt tại A', B', C', D'.
a) Tứ giác A', B', C', D' là hình gì? Chứng minh rằng .
b) Chứng minh rằng điều kiện để tứ giác A', B', C', D' là hình thoi là nó có hai đỉnh đối diện cách đều mặt phẳng (α).
c) Chứng minh rằng điều kiện để tứ giác A', B', C', D' là hình chữ nhật là nó có hai đỉnh kề nhau cách đều mặt phẳng (α).
Cho khối tứ diện đều ABCD cạnh a. Gọi E là điểm đối xứng của A qua D. Mặt phẳng qua CE và vuông góc với mặt phẳng (ABD) cắt cạnh AB tại điểm F. Tính thể tích V của khối tứ diện AECF.
A. 2 a 3 30
B. 2 a 3 60
C. 2 a 3 40
D. 2 a 3 15
Tìm số mặt phẳng đối xứng của tứ diện đều.
A. 4
B. 9
C. 3
D. 6
Cho tứ diện đều ABCD có cạnh bằng a. Gọi E,F lần lượt là các điểm đối xứng của B qua C,D và M là trung điểm của đoạn thẳng AB. Gọi (T) là thiết diện của tứ diện ABCD khi cắt bởi mặt phẳng (MEF). Tính diện tích S của thiết diện (T)
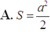


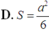
Cho hình chóp tứ diện đều S.ABCD có canh đáy a, cạnh bên hợp với đáy một góc 60 o . Gọi M là điểm đối xứng với C qua D, N là trung điểm của SC, mặt phẳng (BMN) chia khối chóp S.ABCD thành 2 phần. Tính tỉ số thể tích của hai phần đó.
A. 7 5
B. 7 3
C. 1 7
D. 1 5
Số mặt phẳng đối xứng của hình đa diện đều loại {3;4} là:
A. 3
B. 8
C. 9
D. 6