Chọn D.
![]()
![]()
⇒ Hàm số đạt cực tiểu tại x = 0
⇒ Khi m = 0 hàm số không có cực đại
⇒ m = 0 thỏa mãn
![]()
Ta có
![]()
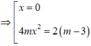
![]()
![]()
Để hàm số y = m x 4 - m - 3 x 2 + m 2 không có điểm cực đại
+) (*) vô nghiệm
![]()
⇒ Hàm số chỉ có 1 cực trị x = 0
Để x = 0 là điểm cực tiểu
![]()
⇔ m < 3
⇒ 0 < m < 3
+) (*) có nghiệm kép x = 0 ⇒ m = 3
Khi đó y ' = 12 x 3 = 0 ⇔ x = 0
Qua điểm x = 0 ta thấy y ' đổi dấu từ âm sang dương
⇒ x = 0 là điểm cực tiểu
⇒ m = 3 thỏa mãn.
+) (*) có 2 nghiệm phân biệt
⇒ Hàm số luôn có cực đại ⇒ Loại.
Vậy để hàm số đã cho không có cực đại thì 0 ≤ m ≤ 3
Mà m ∈ Z ⇒ m ∈ 0 ; 1 ; 2 ; 3






