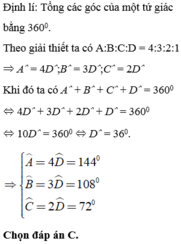Các câu hỏi tương tự
Tứ giác ABCD có số đo góc A75 0 ; góc B115 0 ; góc C 100 0 . Vậy số đo góc D bằngA. 70 0B. 75 0C. 80 0D. 85 0
Đọc tiếp
Tứ giác ABCD có số đo góc A=75 0 ; góc B=115 0 ; góc C = 100 0 . Vậy số đo góc D bằngA. 70 0B. 75 0C. 80 0D. 85 0
Tứ giác ABCD có góc C bằng 600; góc D bằng 600 . Gọi E là giao điểm của các đường phân giác trong của góc A và góc B. Số đo của góc AEB là …0.
Bài 1: Cho tứ giác ABCD có góc B1100 ; góc D 700 , AC là tia phân giác của góc A . Chứng minh rằng CBCDb) Thay điều kiện góc B1100 ; góc D700 trong câu a bởi điều kiện nào để bài toán vẫn đúng Bài 2 : cho tứ giác ABCD có AC900 . Vẽ tia phân giác của góc B cắt AD ở E . Qua D kẻ đường thẳng song song với BE cắt BC tại F . Chứng minh rằng DF là tia phân giác của góc D Bài 3; Cho tứ giác ABCD có góc A1000 ; góc B 1200 . Các tia phân giác của góc C và góc D cắt nhau tại E , các tia phân giác của g...
Đọc tiếp
Bài 1: Cho tứ giác ABCD có góc B=1100 ; góc D = 700 , AC là tia phân giác của góc A . Chứng minh rằng CB=CD
b) Thay điều kiện góc B=1100 ; góc D=700 trong câu a bởi điều kiện nào để bài toán vẫn đúng
Bài 2 : cho tứ giác ABCD có A=C=900 . Vẽ tia phân giác của góc B cắt AD ở E . Qua D kẻ đường thẳng song song với BE cắt BC tại F . Chứng minh rằng DF là tia phân giác của góc D
Bài 3; Cho tứ giác ABCD có góc A=1000 ; góc B = 1200 . Các tia phân giác của góc C và góc D cắt nhau tại E , các tia phân giác của góc ngoài tại C và D cắt nhau tại F . Tính các góc của tứ giác DECF
Bài 4 : Chứng minh rằng 1 tứ giác , tổng 2 đường chéo lớn hơn nửa chu vi và nhỏ hơn chu vi tứ giác đó ( Sử dụng bất đẳng thức )
tìm số đo các góc chưa bt của tứ giác trong từng trường hợp sau:
a) tứ giác có các góc 800, 700 và 2 góc còn lại góc này gấp 2 lần góc kia
b) tứ giác có số đo góc lần lượt tỉ lệ vs 1:2:4:5
Số đo các góc của tứ giác ABCD theo tỷ lệ A:B:C:D 4:3:2:1. Số đo các góc theo thứ tự đó là? A.
120
0
;
90
0
;
72
0
;
36
0
B.
140
0
;
108
0
;
72
0
;
36
0
...
Đọc tiếp
Số đo các góc của tứ giác ABCD theo tỷ lệ A:B:C:D = 4:3:2:1. Số đo các góc theo thứ tự đó là?
A. 120 0 ; 90 0 ; 72 0 ; 36 0
B. 140 0 ; 108 0 ; 72 0 ; 36 0
C. 144 0 ; 108 0 ; 72 0 ; 36 0
D. Cả A, B, C đều sai.
Cho tứ giác ABCD có 6 : 5 : 4 : 3. Tính các góc của tứ giác ABCD.b) Cho tứ giác ABCD có 600, 1200, 800. Tính số đo góc ngoài tại đỉnh A.c) Tính tổng các góc ngoài của tứ giác.d) Chứng minh rằng các góc của tứ giác không thể đều là góc nhọn, không thể đều là góc tù.
Đọc tiếp
Cho tứ giác ABCD có  = 6 : 5 : 4 : 3. Tính các góc của tứ giác ABCD.
= 6 : 5 : 4 : 3. Tính các góc của tứ giác ABCD.
b) Cho tứ giác ABCD có  = 600,
= 600,  = 1200,
= 1200,  = 800. Tính số đo góc ngoài tại đỉnh A.
= 800. Tính số đo góc ngoài tại đỉnh A.
c) Tính tổng các góc ngoài của tứ giác.
d) Chứng minh rằng các góc của tứ giác không thể đều là góc nhọn, không thể đều là góc tù.
Bài 1: Cho tứ giác ABCD biết góc A : B : C : D 1 : 2 : 3 : 4a) Tính các góc của tứ giác ABCDb) Chứng minh: AB // CDc) Gọi giao điểm của AD cắt BC E. Tính các góc của tam giác CDE Bài 2: Cho tứ giác ABCD có góc C 80^0 , D 70^0 . Các tia phân giác của các góc A và B cắt nhau tại I. Tính AIBBài 3: Cho tứ giác ABCD có AB BC; CD DAa) Chứng minh rằng BD là đường trung trực của ACb) Cho biết góc B 100^0 ; D 70^0 . Tính góc A và C
Đọc tiếp
Bài 1: Cho tứ giác ABCD biết góc A : B : C : D = 1 : 2 : 3 : 4
a) Tính các góc của tứ giác ABCD
b) Chứng minh: AB // CD
c) Gọi giao điểm của AD cắt BC = E. Tính các góc của tam giác CDE
Bài 2: Cho tứ giác ABCD có góc C = \(80^0\) , D = \(70^0\) . Các tia phân giác của các góc A và B cắt nhau tại I. Tính AIB
Bài 3: Cho tứ giác ABCD có AB = BC; CD = DA
a) Chứng minh rằng BD là đường trung trực của AC
b) Cho biết góc B = \(100^0\) ; D = \(70^0\) . Tính góc A và C
BÀI 1 : CHO TỨ GIÁC ABCD CÓ : widehat{A}+widehat{B}200^{^0};widehat{B}+widehat{C}218^0;widehat{C}+widehat{D}160^0 TÍNH widehat{C}VÀ widehat{D}BÀI 2 : CHO TỨ GIÁC ABCD CÓ widehat{B}80^0;widehat{D}120^0GÓC NGOÀI ĐỈNH C BẰNG 1300 . TÍNH GÓC A CỦA TỨ GIÁC BÀI 3 : TỨ GIÁC ABCD CÓ widehat{A}57^0;widehat{C}110^0;widehat{D}75^0.TÍNH GÓC NGOÀI TẠI ĐỈNH B
Đọc tiếp
BÀI 1 : CHO TỨ GIÁC ABCD CÓ : \(\widehat{A}+\widehat{B}=200^{^0};\widehat{B}+\widehat{C}=218^0;\widehat{C}+\widehat{D}=160^0\) TÍNH \(\widehat{C}\)VÀ \(\widehat{D}\)
BÀI 2 : CHO TỨ GIÁC ABCD CÓ \(\widehat{B}=80^0;\widehat{D}=120^0\)GÓC NGOÀI ĐỈNH C BẰNG 1300 . TÍNH GÓC A CỦA TỨ GIÁC
BÀI 3 : TỨ GIÁC ABCD CÓ \(\widehat{A}=57^0;\widehat{C}=110^0;\widehat{D}=75^0\).TÍNH GÓC NGOÀI TẠI ĐỈNH B
Cho tứ giác ABCD, biết B = 1300, C= 700, D= 500. Số đo góc A bằng