Các câu hỏi tương tự
Chứng minh rằng : Trung điểm các cạnh của một lục giác đều là đỉnh của một lục giác đều
Gọi a b là số đo 1 góc trong của 2 đa giác đều có số cạnh lần lượt là x và y Cmr:đó là lục giác đều và tam thập lục giác đều
b2 cho biết đa giác đều là đa giác cả tất cả các cạnh bằng nhau tất cả các góc bằng nhau
â) tính số đo mỗi góc của;ngũ giác đều , lục giác đều
b)tính số đo mỗi góc của;1 đa giác đều với n cạnh
Cho lục giác đều MNPQRS (h.bs.27). Gọi X, Y, Z tương ứng là trung điểm của các cạnh MN, PQ và RS. Khi đó XYZ là:(A) tam giác vuông;(B) tam giác vuông cân;(C) tam giác đều;(D) tam giác mà độ dài các cạnh của nó đôi một khác nhau.
Đọc tiếp
Cho lục giác đều MNPQRS (h.bs.27). Gọi X, Y, Z tương ứng là trung điểm của các cạnh MN, PQ và RS. Khi đó XYZ là:
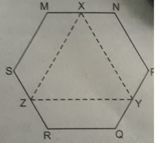
(A) tam giác vuông;
(B) tam giác vuông cân;
(C) tam giác đều;
(D) tam giác mà độ dài các cạnh của nó đôi một khác nhau.
Chứng minh trung điểm 3 cạnh đôi một không kề nhau của một lục giác đều luôn làm thành ba định của 1 tam giác đều
Quan sát hình 120 và điền cụm từ và số thích hợp vào các ô trống ở bảng sau, biết rằng các hình đã cho là những hình chóp đều.
Chóp tam giác đều
Chóp tứ giác đều
Chóp ngũ giác đều
Chóp lục giác đều
Đáy
Tam giác đều
Mặt bên
Tam giác cân
Số cạnh đáy
5
Số cạnh
10
Số mặt
5
Đọc tiếp
Quan sát hình 120 và điền cụm từ và số thích hợp vào các ô trống ở bảng sau, biết rằng các hình đã cho là những hình chóp đều.
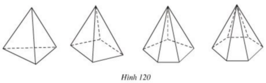
| Chóp tam giác đều | Chóp tứ giác đều | Chóp ngũ giác đều | Chóp lục giác đều | |
| Đáy | Tam giác đều | |||
| Mặt bên | Tam giác cân | |||
| Số cạnh đáy | 5 | |||
| Số cạnh | 10 | |||
| Số mặt | 5 |
Tính diện tích xung quanh , diện tích toàn phần và thể tích của lăng trụ đứng có chiều cao h và cạnh đáy lần lượt là: a)hình vuông cạnh a b)Tam giác đều cạnh a c) lục giác đều cạnh a d) hình thang cân,đáy lớn là 2a,các cạnh còn lại a e) hình thoi có 2 đường chéo là 6a và 8a
diện tích lục giác đều cạnh là 3cm
Tính diện tích toàn phần của:
a) Hình chóp tứ giác đều, biết cạnh đáy a = 5cm, cạnh bên b = 5cm, √18,75 ≈ 4,33;
b) Hình chóp lục giác đều, biết cạnh đáy a = 6cm, cạnh bên b = 10cm, √3 ≈ 1,73; √91 ≈9,54.











