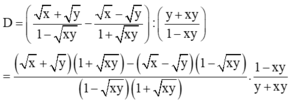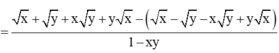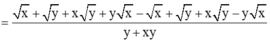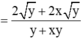Các câu hỏi tương tự
Rút gọn các biểu thức sau:a) Adfrac{xsqrt{y}+ysqrt{x}}{x+2sqrt{xy}+y}(x≥0 , y≥0 , xy≠0)b) Bdfrac{xsqrt{y}-ysqrt{x}}{x-2sqrt{xy}+y}(x≥0 , y≥0 , x≠y)c) Cdfrac{3sqrt{a}-2a-1}{4a-4sqrt{a}+1}(a≥0 , a≠dfrac{1}{4})d) Ddfrac{a+4sqrt{a}+4}{sqrt{a}+2}+dfrac{4-a}{sqrt{a}-2}(a≥0 , a≠4)
Đọc tiếp
Rút gọn các biểu thức sau:
a) A=\(\dfrac{x\sqrt{y}+y\sqrt{x}}{x+2\sqrt{xy}+y}\)(x≥0 , y≥0 , xy≠0)
b) B=\(\dfrac{x\sqrt{y}-y\sqrt{x}}{x-2\sqrt{xy}+y}\)(x≥0 , y≥0 , x≠y)
c) C=\(\dfrac{3\sqrt{a}-2a-1}{4a-4\sqrt{a}+1}\)(a≥0 , a≠\(\dfrac{1}{4}\))
d) D=\(\dfrac{a+4\sqrt{a}+4}{\sqrt{a}+2}+\dfrac{4-a}{\sqrt{a}-2}\)(a≥0 , a≠4)
Rút gọn:a/ frac{left(sqrt{x^2+9}-3right)left(sqrt{x^2+9}+3right)left(x+sqrt{xy}+yright)sqrt{x-2sqrt{xy}+y}}{xleft(xsqrt{x}-ysqrt{y}right)} (với x0, yge0, xney b/ left[left(frac{1}{sqrt{x}}+frac{1}{sqrt{y}}right).frac{2}{sqrt{x}+sqrt{y}}+frac{1}{sqrt{x}}+frac{1}{sqrt{y}}right]:frac{sqrt{x^3}+ysqrt{x}+xsqrt{y}+sqrt{y^3}}{sqrt{x^3y}+sqrt{xy^3}}(với x0 và xne1 c/ left(frac{sqrt{x}+1}{sqrt{xy}+1}+frac{sqrt{xy}+sqrt{x}}{1-sqrt{xy}}+1right):left(1-frac{sqrt{xy}+sqrt{x}}{sqrt{xy}-1}-frac{sqrt{x}+1}{sqrt...
Đọc tiếp
Rút gọn:
a/ \(\frac{\left(\sqrt{x^2+9}-3\right)\left(\sqrt{x^2+9}+3\right)\left(x+\sqrt{xy}+y\right)\sqrt{x-2\sqrt{xy}+y}}{x\left(x\sqrt{x}-y\sqrt{y}\right)}\) (với x>0, y\(\ge\)0, x\(\ne\)y
b/ \(\left[\left(\frac{1}{\sqrt{x}}+\frac{1}{\sqrt{y}}\right).\frac{2}{\sqrt{x}+\sqrt{y}}+\frac{1}{\sqrt{x}}+\frac{1}{\sqrt{y}}\right]:\frac{\sqrt{x^3}+y\sqrt{x}+x\sqrt{y}+\sqrt{y^3}}{\sqrt{x^3y}+\sqrt{xy^3}}\)(với x>0 và x\(\ne\)1
c/ \(\left(\frac{\sqrt{x}+1}{\sqrt{xy}+1}+\frac{\sqrt{xy}+\sqrt{x}}{1-\sqrt{xy}}+1\right):\left(1-\frac{\sqrt{xy}+\sqrt{x}}{\sqrt{xy}-1}-\frac{\sqrt{x}+1}{\sqrt{xy}+1}\right)\)(với x>0 và x\(\ne\)1
Rút gọn biểu thức A:
\(A=\left(\frac{\sqrt{x}+1}{\sqrt{xy}+1}+\frac{\sqrt{xy}+\sqrt{x}}{1-\sqrt{xy}}+1\right):\left(1-\frac{\sqrt{xy}+\sqrt{x}}{\sqrt{xy}-1}-\frac{\sqrt{x}+1}{\sqrt{xy}+1}\right)\)với \(x>0,\)\(y>0,\)\(xy\ne1\)
Cho biểu thức
A = \(\left(\frac{\sqrt{x}}{x+\sqrt{xy}}+\frac{\sqrt{y}}{y-\sqrt{xy}}\right):\frac{2\sqrt{xy}}{x-y}\)
(x>0; y>0; x khác y)
a. Rút gọn A
b. Tìm giá trị của x và y để A =1
Rút gọn biểu thức sau:
\(A=\frac{x+y+2\sqrt{xy}}{\sqrt{xy}+x}.\frac{x+y-2\sqrt{xy}}{\sqrt{xy}-y}\) với xy > hoặc = 0 và x # y
Rút gọn\(A=\left(\frac{\sqrt{x}+\sqrt{y}}{1-\sqrt{xy}}+\frac{\sqrt{x}-\sqrt{y}}{1+\sqrt{xy}}\right):\left(1+\frac{x+y+2xy}{1-xy}\right)\)
35Cho biểu thứcPleft[left(frac{1}{sqrt{x}}+frac{1}{sqrt{y}}right)frac{2}{sqrt{x}+sqrt{y}}+frac{1}{x}+frac{1}{y}right]:frac{sqrt{x^3}+ysqrt{x}+xsqrt{y}+sqrt{y^3}}{sqrt{xy^3}+sqrt{x^3y}}a) Rút gọn Pb)Cho xy16 . Tìm Min P 34 Cho biểu thức Pfrac{x}{sqrt{xy}-2y}-frac{2sqrt{x}}{x+sqrt{x}-2sqrt{xy}-2sqrt{y}}-frac{1-x}{1-sqrt{x}}a) Rút gọn Pb)Tính P biết 2x^2+y^2-4x-2xy+40
Đọc tiếp
35Cho biểu thức
P=\(\left[\left(\frac{1}{\sqrt{x}}+\frac{1}{\sqrt{y}}\right)\frac{2}{\sqrt{x}+\sqrt{y}}+\frac{1}{x}+\frac{1}{y}\right]:\frac{\sqrt{x^3}+y\sqrt{x}+x\sqrt{y}+\sqrt{y^3}}{\sqrt{xy^3}+\sqrt{x^3y}}\)
a) Rút gọn P
b)Cho xy=16 . Tìm Min P
34 Cho biểu thức
P=\(\frac{x}{\sqrt{xy}-2y}-\frac{2\sqrt{x}}{x+\sqrt{x}-2\sqrt{xy}-2\sqrt{y}}-\frac{1-x}{1-\sqrt{x}}\)
a) Rút gọn P
b)Tính P biết 2x^2+y^2-4x-2xy+4=0
cho biểu thức: Pleft(frac{sqrt{x}+1}{sqrt{xy}+1}+frac{sqrt{xy}+sqrt{x}}{1-sqrt{xy}}+1right):left(1-frac{sqrt{xy}+sqrt{x}}{sqrt{xy}-1}-frac{sqrt{x}+1}{sqrt{xy}+1}right) Pleft(frac{sqrt{x}+1}{sqrt{xy}+1}+frac{sqrt{xy}+sqrt{x}}{1-sqrt{xy}}+1right):left(1-frac{sqrt{xy}+1}{sqrt{xy}-1}-frac{sqrt{x}+1}{sqrt{xy}+1}right).backslash với x,yge0;x,yne1 a) Rút gọn Pb) Tính P khi xsqrt[3]{4-2sqrt{6}}+sqrt[3]{4+2sqrt{6}}và yx^2+6
Đọc tiếp
cho biểu thức: \(P=\left(\frac{\sqrt{x}+1}{\sqrt{xy}+1}+\frac{\sqrt{xy}+\sqrt{x}}{1-\sqrt{xy}}+1\right):\left(1-\frac{\sqrt{xy}+\sqrt{x}}{\sqrt{xy}-1}-\frac{\sqrt{x}+1}{\sqrt{xy}+1}\right)\) \(P=\left(\frac{\sqrt{x}+1}{\sqrt{xy}+1}+\frac{\sqrt{xy}+\sqrt{x}}{1-\sqrt{xy}}+1\right):\left(1-\frac{\sqrt{xy}+1}{\sqrt{xy}-1}-\frac{\sqrt{x}+1}{\sqrt{xy}+1}\right).\backslash\ \)với \(x,y\ge0;x,y\ne1\)
a) Rút gọn P
b) Tính P khi \(x=\sqrt[3]{4-2\sqrt{6}}+\sqrt[3]{4+2\sqrt{6}}\)và \(y=x^2+6\)
Bài 1: Rút gọn các biểu thức sau: a)√(5+2√5)² - √5 ______ √5+2 b) x-2 √xy + y _______________ X - Y (x khác y , x > hoặc = 0 , y > hoặc = 0 )