Các câu hỏi tương tự
Cho (O;R) và dây cung BC cố định (BC2R).Điểm A di động trên đường tròn sao cho tam giác ABC nhọn,Gọi AD là đường cao của tam giác ABC và H là trực tâm tam giác ABCa)Đường thẳng chứa tia phân giác góc ngoài góc BHC cắt AB,AC lần lượt tại M,N.Chưng minh tam giác AMN cânb)Gọi E,F lần lượt là hình chiếu của D trên BH,CH.Chứng minh OA vuông goác với EFc)Đường tròn ngoại tiếp tam giác AMN cắt đường phân giác góc trong của goác BAC tại K.Chứng minh rằng đường thẳng HK luôn đi qua 1 điểm cố định
Đọc tiếp
Cho (O;R) và dây cung BC cố định (BC<2R).Điểm A di động trên đường tròn sao cho tam giác ABC nhọn,Gọi AD là đường cao của tam giác ABC và H là trực tâm tam giác ABC
a)Đường thẳng chứa tia phân giác góc ngoài góc BHC cắt AB,AC lần lượt tại M,N.Chưng minh tam giác AMN cân
b)Gọi E,F lần lượt là hình chiếu của D trên BH,CH.Chứng minh OA vuông goác với EF
c)Đường tròn ngoại tiếp tam giác AMN cắt đường phân giác góc trong của goác BAC tại K.Chứng minh rằng đường thẳng HK luôn đi qua 1 điểm cố định
Cho tam giác ABC cân ở A , góc A nhọn. Đường vuông góc với AB tại A cắt đường thẳng BC ở E. Kẻ EN vuông góc vs AC. Gọi M là trung điểm BC. Hai đường thẳng AM và EN cắt nhau ở F.
a, Tìm nhữg tứ giác có thể nội tiếp đường tròn. Giải thích vì sao? Xác định tâm các đường tròn đó
b, CM: EB là tia phân giác của góc AEF
c, CM: M là tâm đường tròn ngoại tiếp tam giác AFN
Cho tam giác ABC cân tại A, có O là trung điểm BC và BC2a. Đường tròn tâm O tiếp xúc với AB, AC lần lượt tại H và T. Qua D trên cung nhỏ HT, kẻ tiếp tuyến với (O) cắt AB và AC ở M và Na) Xác định tâm I của đường tròn ngoại tiếp tam giác AHTb) Chứng minh góc MON góc ABCc) Tính tích BM.CN theo ad) Định vị trí của MN sao cho BM+CN đạt giá trị nhỏ nhấtGiup với mình tick cho
Đọc tiếp
Cho tam giác ABC cân tại A, có O là trung điểm BC và BC=2a. Đường tròn tâm O tiếp xúc với AB, AC lần lượt tại H và T. Qua D trên cung nhỏ HT, kẻ tiếp tuyến với (O) cắt AB và AC ở M và N
a) Xác định tâm I của đường tròn ngoại tiếp tam giác AHT
b) Chứng minh góc MON= góc ABC
c) Tính tích BM.CN theo a
d) Định vị trí của MN sao cho BM+CN đạt giá trị nhỏ nhất
Giup với mình tick cho
Cho đường tròn tâm O đường kính AB, gọi K là điểm chính giữa của cung AB, M di động trên cung nhỏ AK ( M khác A và K). Lấy điểm N trên đoạn BM sao cho BN AMa) chứng minh góc AMK góc BNKb) Chứng minh tâm giác MNk là tam giác vuông cânc) hai đươngt hẳng AM và OK cắt nhau tại D, chứng minh MK là tia phân giác của góc DMNd) Chứng minh đường thẳng vuông góc tại BM tại N luôn đi qua 1 điểm cố định
Đọc tiếp
Cho đường tròn tâm O đường kính AB, gọi K là điểm chính giữa của cung AB, M di động trên cung nhỏ AK ( M khác A và K). Lấy điểm N trên đoạn BM sao cho BN = AM
a) chứng minh góc AMK = góc BNK
b) Chứng minh tâm giác MNk là tam giác vuông cân
c) hai đươngt hẳng AM và OK cắt nhau tại D, chứng minh MK là tia phân giác của góc DMN
d) Chứng minh đường thẳng vuông góc tại BM tại N luôn đi qua 1 điểm cố định
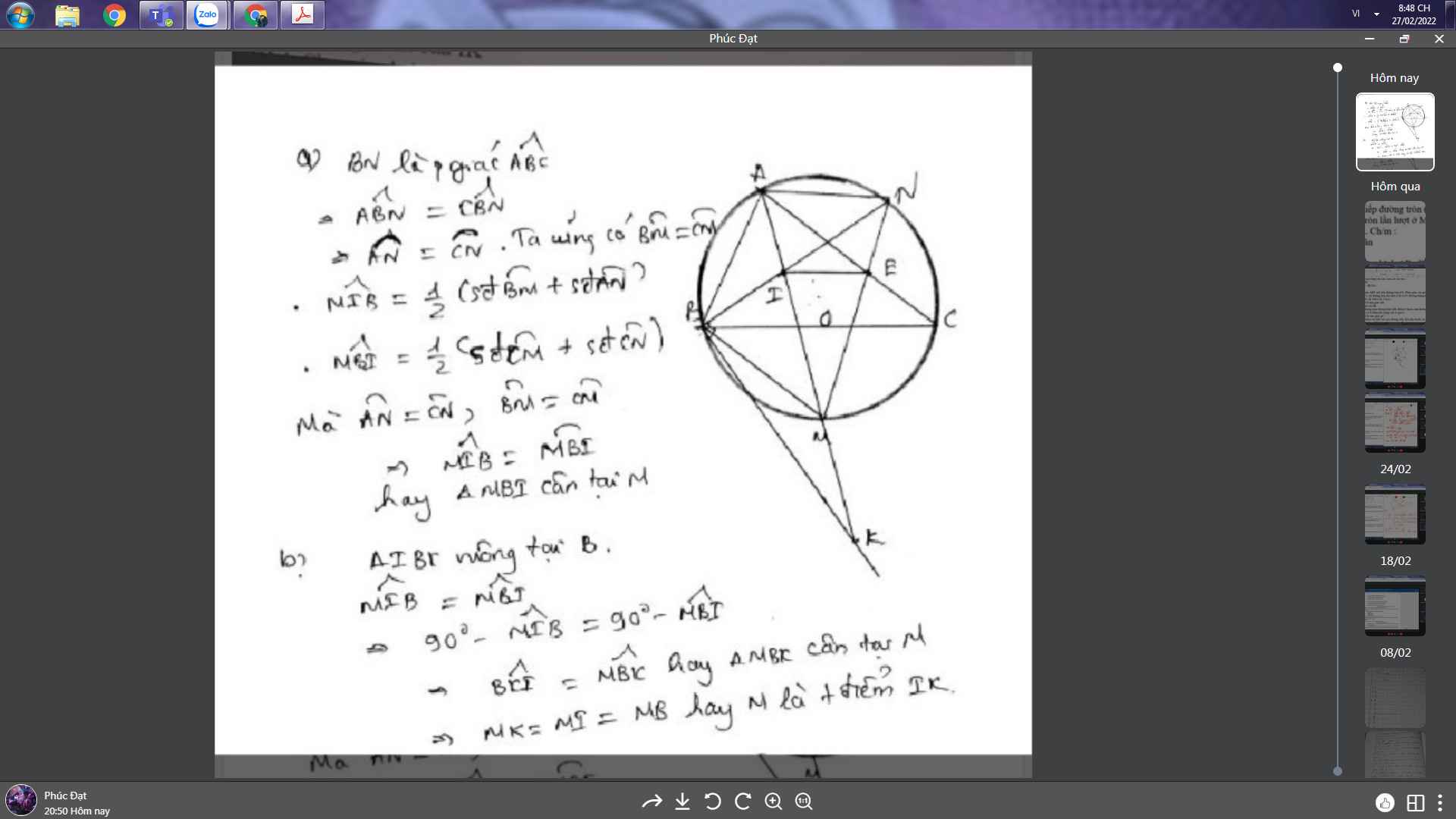
từ điểm M ở ngoài đường tròn (O) kẻ các tiếp tuyến MA, MB. lấy điểm trên cung nhỏ AB và kẻ đường thẳng MC cắt đường tròn (O) tại điểm thứ hai D. Tia phân giác cảu góc DBC cắt CD tại E. Gọi I trung điểm của dây CD. c/m:
a) Tam giác MEB cân
b) AE là đường phân giác của tam giác ACD
c) IM là tia phân giác của góc AIB
Cho tam giác ABC vuông tại A , đường trung tuyến AM . Qua A kẻ đường thẳng vuông góc với AM cắt đường thẳng vuông góc với BC tại B ở D , cắt đường thẳng vuông góc với BC tại C ở E . Tia EM cắt tia DB ở I . gọi P và Q lần lượt là giao điểm của AB và DM của AC và ME . Chứng minh :a. Tam giác MCE tam giác MBIb. Tam giác DIE là tam giác cânc. DE BD+CEd. PQ song song với BC và PQ 1/2 BC
Đọc tiếp
Cho tam giác ABC vuông tại A , đường trung tuyến AM . Qua A kẻ đường thẳng vuông góc với AM cắt đường thẳng vuông góc với BC tại B ở D , cắt đường thẳng vuông góc với BC tại C ở E . Tia EM cắt tia DB ở I . gọi P và Q lần lượt là giao điểm của AB và DM của AC và ME . Chứng minh :
a. Tam giác MCE = tam giác MBI
b. Tam giác DIE là tam giác cân
c. DE = BD+CE
d. PQ song song với BC và PQ = 1/2 BC
Cho đường tròn (o) , đường kính AB 4cm . Lấy điểm C thuộc (o) sao cho góc CAB 30 độ ; M là điểm chính giữa cung nhỏ AC . Các đường thẳng Am và BC căt nhau tại I , các đường thẳng AC và BM cắt nhau tại Ka) Chứng minh góc ABM góc IBM và tam giác ABI cânb) Chứng minh tứ giác MICK nội tiếpC) Đường thẳng BM cắt tiếp tuyến tại A của (O) ở N . Chứng minh đường thẳng NI là tiếp tuyển của đường tròn (B ;BA)d) Tính diện tích hình quạt COB ( ứng với cing nhỏ CB )
Đọc tiếp
Cho đường tròn (o) , đường kính AB = 4cm . Lấy điểm C thuộc (o) sao cho góc CAB = 30 độ ; M là điểm chính giữa cung nhỏ AC . Các đường thẳng Am và BC căt nhau tại I , các đường thẳng AC và BM cắt nhau tại K
a) Chứng minh góc ABM = góc IBM và tam giác ABI cân
b) Chứng minh tứ giác MICK nội tiếp
C) Đường thẳng BM cắt tiếp tuyến tại A của (O) ở N . Chứng minh đường thẳng NI là tiếp tuyển của đường tròn (B ;BA)
d) Tính diện tích hình quạt COB ( ứng với cing nhỏ CB )
Cho tam giác vuông ABC vuông tại A, với ACAB, AH là đường cao kẻ từ đỉnh A. Các tiếp tuyến tại A và B với đường tròn (O) ngoại tiếp tam giác ABC cắt nhau tại M. Đoạn MO cắt cạnh AB ở E. Đoạn MC cắt đường cao AH tại F. Kéo dài CA cắt đường thẳng BM ở D. Đường thẳng BF cắt đường thẳng AM ở N.(1. C/m OM//CD và M là trung điểm của BD)2. C/m EF//BC3, C/m HA là tia phân giác góc MHN4, Trên tia BA lấy điểm K sao cho BK3.BA. Kẻ đường thẳng Ky vuông góc với KC tại K cắt BD tại G. C/m tam giác AKG cân.
Đọc tiếp
Cho tam giác vuông ABC vuông tại A, với AC<AB, AH là đường cao kẻ từ đỉnh A. Các tiếp tuyến tại A và B với đường tròn (O) ngoại tiếp tam giác ABC cắt nhau tại M. Đoạn MO cắt cạnh AB ở E. Đoạn MC cắt đường cao AH tại F. Kéo dài CA cắt đường thẳng BM ở D. Đường thẳng BF cắt đường thẳng AM ở N.
(1. C/m OM//CD và M là trung điểm của BD)
2. C/m EF//BC
3, C/m HA là tia phân giác góc MHN
4, Trên tia BA lấy điểm K sao cho BK=3.BA. Kẻ đường thẳng Ky vuông góc với KC tại K cắt BD tại G. C/m tam giác AKG cân.
Cho đường tròn (O), dây cung AB. Qua O kẻ đường thẳng vuông góc với AB cắt tiếp tuyến tại A của đường tròn tam O ở điểm C. Kẻ đường kính BOD của đường tròn (O), gọi giao điểm của OC với đường tròn (O) là M. Chứng minh BM là tia phân giác của góc CBA