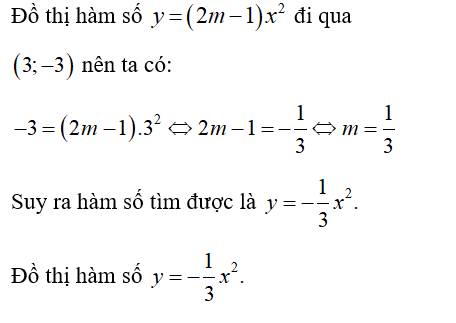Em nghĩ nên sửa đề thành Parabol đi qua điểm (3;3) thì bài toán mới giải được ạ
Parabol đi qua điểm (3;3) nên ta có:
\(3=\left(2m-1\right)\cdot3^2\Rightarrow2m-1=\frac{1}{3}\)
\(\Leftrightarrow2m=\frac{4}{3}\Rightarrow m=\frac{2}{3}\)
Khi đó ta được parabol \(y=\frac{x^2}{3}\)
Đường thẳng song song với trục hoành cắt trục tung tại điểm có tung độ là 4 => y = 4
Khi đó \(4=\frac{x^2}{3}\Rightarrow x^2=12\Rightarrow\orbr{\begin{cases}x=2\sqrt{3}\\x=-2\sqrt{3}\end{cases}}\)
G/s A nằm ở phía dương, B ở phía âm đối với trục hoành thì khi đó tọa độ của A và B là: \(\hept{\begin{cases}A\left(2\sqrt{3};4\right)\\B\left(-2\sqrt{3};4\right)\end{cases}}\)
\(\Rightarrow AB=\left|2\sqrt{3}\right|+\left|-2\sqrt{3}\right|=4\sqrt{3}\)
\(\Rightarrow S_{OAB}=\frac{4\sqrt{3}\cdot4}{2}=8\sqrt{3}\left(dvdt\right)\)
Ta có : Parabol y=(2m-1)x\(^2\) đi qua điểm (3;-3)
⇒-3=(2m-1)3\(^2\)
⇒-3=18m - 9
⇒18m=6
⇒m=\(\dfrac{1}{3}\)
⇒y=-\(\dfrac{1}{3}\)x\(^2\)
vì parabol đi qua điểm (3;-3) nên ta có -3=(2m-1)9
suy ra m=1/3 suy ra y=-1/3x2
đường thẳng // với trục hoành cắt trục tung tại điểm có tung độ bằng 4 .Suy ra y=4
khi đó 4=-1/3x2
suy ra x2=-12 (vô lý)
Parabol y=(2m-1)x đi qua điểm (3;-3)
\(\Rightarrow\) Parabol có dạng y=\(\dfrac{1}{3}\)x2
gọi H là giao của AB với Oy\(\Rightarrow\)OH = 4(AB cắt Oy tậu điểm có tung độ là 4)
Có điểm A thuộc parabol
y=\(\dfrac{1}{3}\)x2 và có tung độ là 4\(\Rightarrow\)
A(\(-\sqrt{12}\) ;4)\(\Rightarrow\)AH =\(\sqrt{12}\)
Tương tự vối điểm B ở bên phải trục Oy ta có BH\(\sqrt{12}\)
Có AB =AH+BH=2\(\sqrt{12}\)
SAOB= 8\(\sqrt{3}\)(đvdt)
\(\left(P\right):y=\left(2m-1\right).x^2\)
+) Vì parabol đi qua điểm (3 ; -3)
\(\Rightarrow x=3;y=-3.\)
+) Thay \(x=3;y=-3\) vào parabol \(y=\left(2m-1\right).x^2\) ta được:
\(-3=\left(2m-1\right).3^2\)
\(\Leftrightarrow\left(2m-1\right).9=-3\)
\(\Leftrightarrow2m-1=-\dfrac{1}{3}\)
\(\Leftrightarrow2m=\dfrac{2}{3}\)
\(\Leftrightarrow m=\dfrac{1}{3}\)
Khi đó ta có parabol \(y=\left(2.\dfrac{1}{3}-1\right).x^2\)
\(\Rightarrow\left(P\right):y=-\dfrac{1}{3}x^2\)
+) Vì đường thẳng song song với trục hoành cắt trục tung tại điểm có tung độ bằng -4.
\(\Rightarrow y=-4.\)
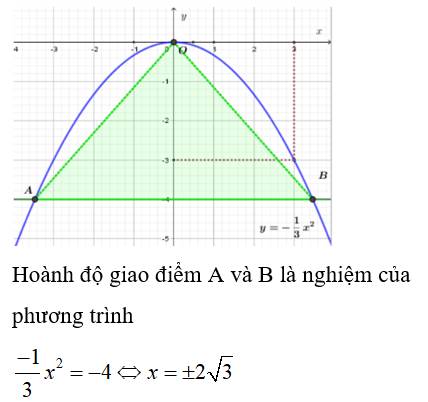
+) Hoành độ giao điểm của A và B là nghiệm của phương trình:
\(-\dfrac{1}{3}x^2=-4\)
\(\Leftrightarrow x^2=\left(-4\right):\left(-\dfrac{1}{3}\right)\)
\(\Leftrightarrow x^2=12\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\sqrt{3}\\x=-2\sqrt{3}\end{matrix}\right.\)
+) Giả sử A nằm ở phía dương, B nằm ở phía âm đối với trục hoành.
=> Tọa độ của A và B là: \(\left\{{}\begin{matrix}A\left(2\sqrt{3};4\right)\\B\left(-2\sqrt{3};4\right)\end{matrix}\right.\)
+) Gọi H là giao điểm của AB và trục tung Oy.
\(\Rightarrow OH=4.\)
+) Ta có: \(\left\{{}\begin{matrix}A\left(2\sqrt{3};4\right)\Rightarrow AH=\left|2\sqrt{3}\right|=2\sqrt{3}\\B\left(-2\sqrt{3};4\right)\Rightarrow BH=\left|-2\sqrt{3}\right|=2\sqrt{3}\end{matrix}\right.\)
+) Lại có: \(AB=AH+BH\)
\(\Rightarrow AB=2\sqrt{3}+2\sqrt{3}\)
\(\Rightarrow AB=4\sqrt{3}\)
Diện tích của tam giác AOB là:
\(S_{AOB}=\dfrac{1}{2}AB.OH=\dfrac{1}{2}.4\sqrt{3}.4=8\sqrt{3}\) (đvđd).
Vậy diện tích của tam giác AOB là: \(8\sqrt{3}\) (đvđd).
thay toạ độ điểm ( 3; -3) vào phương trình \(m=\dfrac{1}{3}\)
hoành độ của A và B là các nghiệm của phương trình \(\dfrac{-1}{3}x^2\) = -4
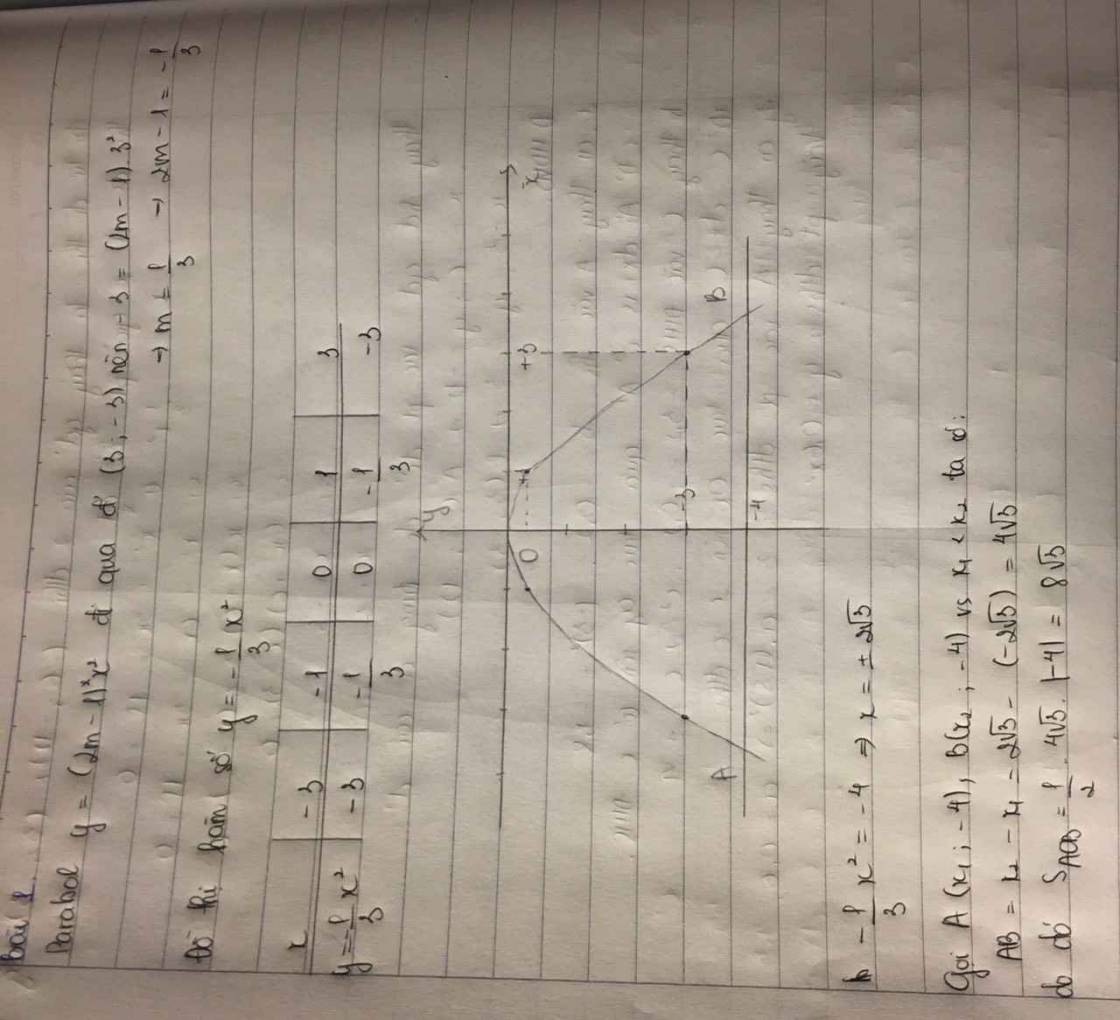
Ta có-1/2x2 =-4 => x= +_2\(\sqrt{3}\). Gọi A(x2 ; -4) với x1< x2 , ta có AB =x1-x2 = 2\(\sqrt{3}\) _ (-2\(\sqrt{3}\)) =4\(\sqrt{3}\) Do đó SAOB=1/2.4\(\sqrt{3}\) .|-4| = 8\(\sqrt{3}\)
Thay toạ độ điểm (3;-3) vào pt 3=(2m-1).3=>2m-1 =1phần3 <=> 2m=4phần3=>m=2phần3 y=x trên 3 4x=>x=12=>x=2 căn 3 x=-2 căn 3 =>AB=|2căn3|+|-2căn3|=4căn3 =>Soab=4căn3.4 trên 2 =8căn3
Y=(2m-1)x2 qua điểm (3;-3) tức là x=3;y=-3 thay x=3 ;y=3 vào Parabol ta có
3=(2m-1)(-3)2
=>m=12/8
Vậy parbol có dạng y=12/8x2
Vì parabol đi qua điểm (3;-3) ⇒ x=3;y=-3
Thay x=3;y=-3 vào parabol ta có:
(2m-1).32=-3
⇔(2m-1).9=-3
⇔2m-1=-1/3
⇔2m=2/3⇔m =1/3
Parabol ⇒ -3=(2m-1).32 ⇒ parabol có dạng y=\(\dfrac{1}{3}\)x2
Điểm A và B có trên parabol có tung độ 4 ⇒ y=\(\dfrac{1}{3}\)x2=4 ⇒ x=+- 2\(\sqrt{3}\)
Diện tích tam giác AOB là \(\dfrac{1}{2}\).4.4\(\sqrt{3}\)= 8\(\sqrt{3}\)