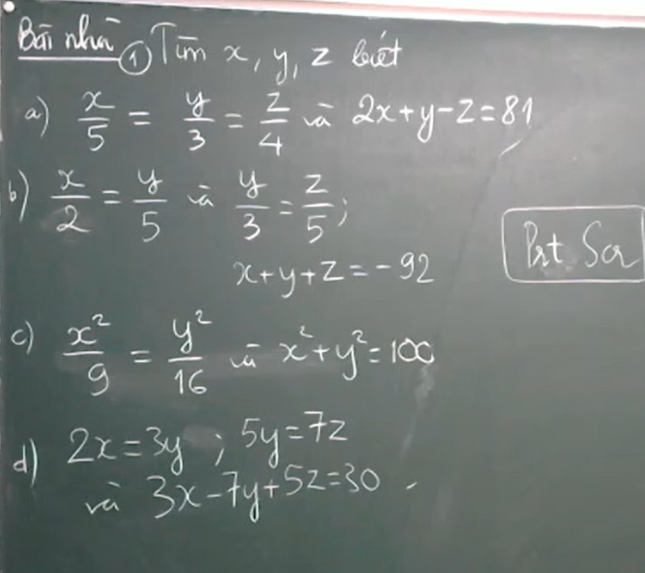a) Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\frac{x}{2}=\frac{y}{3}=\frac{z}{5}=\frac{x+y+z}{2+3+5}=\frac{90}{10}=9\)
\(\Leftrightarrow\hept{\begin{cases}x=9.2=18\\y=9.3=27\\z=9.5=45\end{cases}}\)
b) \(2x=3y\Leftrightarrow\frac{x}{15}=\frac{y}{10},2y=5z\Leftrightarrow\frac{y}{10}=\frac{z}{4}\)
suy ra \(\frac{x}{15}=\frac{y}{10}=\frac{z}{4}\).
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\frac{x}{15}=\frac{y}{10}=\frac{z}{4}=\frac{x-z}{15-4}=\frac{11}{11}=1\)
\(\Leftrightarrow\hept{\begin{cases}x=15.1=15\\y=10.1=10\\z=4.1=4\end{cases}}\)
c) \(\frac{x}{y}=\frac{3}{4}\Leftrightarrow\frac{x}{9}=\frac{y}{12},\frac{y}{z}=\frac{3}{5}\Leftrightarrow\frac{y}{12}=\frac{z}{20}\)
suy ra \(\frac{x}{9}=\frac{y}{12}=\frac{z}{20}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\frac{x}{9}=\frac{y}{12}=\frac{z}{20}=\frac{2x-3y+z}{2.9-3.12+20}=\frac{6}{2}=3\)
\(\Leftrightarrow\hept{\begin{cases}x=3.9=27\\y=3.12=36\\z=3.20=60\end{cases}}\)