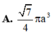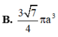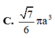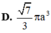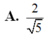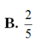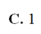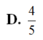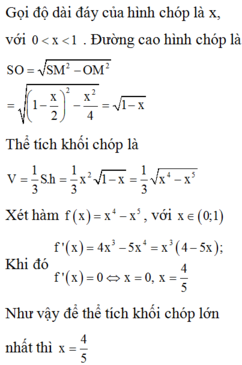Các câu hỏi tương tự
Cắt một miếng giấy hình vuông và xếp thành một hình chóp tứ giác đều (hình vẽ). Biết cạnh hình vuông bằng 20 (cm), OM=x (cm). Tìm x để hình chóp đều ấy có thể tích lớn nhất.
A. 9cm
B. 8cm
C. 6cm
D. 7cm
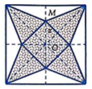
Một tấm nhôm hình vuông cạnh 10cm, người ta cắt ở bốn góc của tấm nhôm đó bốn tam giác cân bằng nhau (xem hình vẽ), mỗi tam giác cân có chiều cao bằng x, rồi gấp tấm nhôm đó dọc theo đường nét đứt để được một hình chóp tứ giác đều. Tìm x để khối chóp nhận được có thể tích lớn nhất. A. x 4 B. x 2 C. x 1 D.
x
3
4
Đọc tiếp
Một tấm nhôm hình vuông cạnh 10cm, người ta cắt ở bốn góc của tấm nhôm đó bốn tam giác cân bằng nhau (xem hình vẽ), mỗi tam giác cân có chiều cao bằng x, rồi gấp tấm nhôm đó dọc theo đường nét đứt để được một hình chóp tứ giác đều. Tìm x để khối chóp nhận được có thể tích lớn nhất.
A. x = 4
B. x = 2
C. x = 1
D. x = 3 4
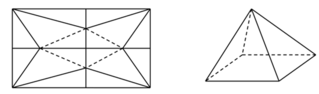
Từ một miếng bìa hình vuông có cạnh bằng 5, người ta cắt 4 góc bìa 4 tứ giác bằng nhau và gập lại phần còn lại của tấm bìa để được một khối chóp tứ giác đều có cạnh đáy bằng x (xem hình vẽ bên). Cho chiều cao khối chóp tứ giác đều này bằng
5
2
. Tính giá trị của x A. x 1 B. x 2 C. x 3 D. x 4
Đọc tiếp
Từ một miếng bìa hình vuông có cạnh bằng 5, người ta cắt 4 góc bìa 4 tứ giác bằng nhau và gập lại phần còn lại của tấm bìa để được một khối chóp tứ giác đều có cạnh đáy bằng x (xem hình vẽ bên). Cho chiều cao khối chóp tứ giác đều này bằng 5 2 . Tính giá trị của x

A. x = 1
B. x = 2
C. x = 3
D. x = 4
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, hình chiếu vuông góc của đỉnh S trên đáy là điểm H trên cạnh AC sao cho
A
H
2
3
A
C
, đường thẳng SB tạo với mặt phẳng đáy một góc
45
0
. Tính thể tích V của khối chóp S.ABC.
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, hình chiếu vuông góc của đỉnh S trên đáy là điểm H trên cạnh AC sao cho A H = 2 3 A C , đường thẳng SB tạo với mặt phẳng đáy một góc 45 0 . Tính thể tích V của khối chóp S.ABC.
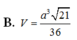
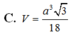
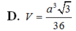
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, hình chiếu vuông góc của đỉnh S trên đáy là điểm H trên cạnh AC sao cho
A
H
2
3
A
C
đường thẳng SC tạo với mặt phẳng đáy một góc
60
0
. Tính thể tích V của khối chóp S.ABC.
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, hình chiếu vuông góc của đỉnh S trên đáy là điểm H trên cạnh AC sao cho A H = 2 3 A C đường thẳng SC tạo với mặt phẳng đáy một góc 60 0 . Tính thể tích V của khối chóp S.ABC.
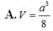
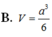
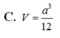

Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng 2a. Mặt phẳng qua AB và trung điểm M của SC cắt hình chóp theo một thiết diện có chu vi bằng 7a. Thể tích khối nón có đỉnh S và đường tròn đáy ngoại tiếp ABCD là: A.
πa
3
6
4
B.
πa
3
3...
Đọc tiếp
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng 2a. Mặt phẳng qua AB và trung điểm M của SC cắt hình chóp theo một thiết diện có chu vi bằng 7a. Thể tích khối nón có đỉnh S và đường tròn đáy ngoại tiếp ABCD là:
A. πa 3 6 4
B. πa 3 3 3
C. πa 3 6 6
D. 2 πa 3 6 3
Cho hình chóp tứ giác đều S.ABCD có đáy là hình vuông tâm O cạnh 2a. Thể tích khối chóp S.ABCD bằng
4
a
3
. Tính khoảng cách từ điểm O tới mặt bên của hình chóp.
Đọc tiếp
Cho hình chóp tứ giác đều S.ABCD có đáy là hình vuông tâm O cạnh 2a. Thể tích khối chóp S.ABCD bằng 4 a 3 . Tính khoảng cách từ điểm O tới mặt bên của hình chóp.
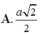
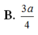
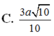
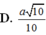
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, diện tích mỗi mặt bên bằng
2
a
2
. Tính thể tích khối nón có đỉnh là S và có đáy là đường tròn ngoại tiếp hình vuông ABCD
Đọc tiếp
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, diện tích mỗi mặt bên bằng 2 a 2 . Tính thể tích khối nón có đỉnh là S và có đáy là đường tròn ngoại tiếp hình vuông ABCD
![]()
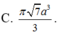
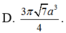
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, diện tích mỗi mặt bên bằng 2a3. Thể tích khối nón có đỉnh S và đường tròn đáy ngoại tiếp hình vuông ABCD bằng
Đọc tiếp
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, diện tích mỗi mặt bên bằng 2a3. Thể tích khối nón có đỉnh S và đường tròn đáy ngoại tiếp hình vuông ABCD bằng