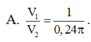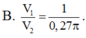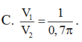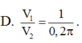Các câu hỏi tương tự
Người ta thiết kế một thùng chứa hình trụ có thể tích V cho trước. Biết rằng đơn giá của vật liệu làm mặt đáy và nắp của thùng bằng nhau và gấp lần đơn giá của vật liệu để làm mặt xung quanh của thùng (chi phí cho mỗi đơn vị diện tích). Gọi chiều cao của thùng là h và bán kính đáy là r. Tính tỉ số
h
r
sao cho chi phí vật liệu sản suất thùng là nhỏ nhất. A.
h
r...
Đọc tiếp
Người ta thiết kế một thùng chứa hình trụ có thể tích V cho trước. Biết rằng đơn giá của vật liệu làm mặt đáy và nắp của thùng bằng nhau và gấp lần đơn giá của vật liệu để làm mặt xung quanh của thùng (chi phí cho mỗi đơn vị diện tích). Gọi chiều cao của thùng là h và bán kính đáy là r. Tính tỉ số h r sao cho chi phí vật liệu sản suất thùng là nhỏ nhất.
A. h r = 2
B. h r = 2
C. h r = 6
D. h r = 3 2
Người ta muốn dùng vật liệu bằng kim loại để gò thành một thùng hình trụ tròn xoay có hai đáy với thể tích V cho trước ( hai đáy cũng dùng chính vật liệu đó). Hãy xác định chiều cao h và bán kính R của hình trụ theo V để tốn ít vật liệu nhất.
Đọc tiếp
Người ta muốn dùng vật liệu bằng kim loại để gò thành một thùng hình trụ tròn xoay có hai đáy với thể tích V cho trước ( hai đáy cũng dùng chính vật liệu đó). Hãy xác định chiều cao h và bán kính R của hình trụ theo V để tốn ít vật liệu nhất.
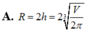
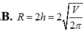
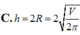
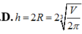
Một người thợ thủ công cần làm một cái thùng hình hộp đứng không nắp đáy là hình vuông có thể tích 100
c
m
3
. Để tiết kiệm vật liệu làm thùng, người đó cần thiết kế sao cho tổng S của diện tích xung quanh và diện tích mặt đáy là nhỏ nhất A. S
30
40
3
B. S
40
40...
Đọc tiếp
Một người thợ thủ công cần làm một cái thùng hình hộp đứng không nắp đáy là hình vuông có thể tích 100 c m 3 . Để tiết kiệm vật liệu làm thùng, người đó cần thiết kế sao cho tổng S của diện tích xung quanh và diện tích mặt đáy là nhỏ nhất
A. S = 30 40 3
B. S = 40 40 3
C. S = 10 40 3
D. S = 20 40 3
Để làm một thùng phi hình trụ người ta cần hai miếng nhựa hình tròn làm hai đáy có diện tích mỗi hình là 4π(c
m
2
) và một miếng nhựa hình chữ nhật có diện tích là 15π(c
m
2
) để làm thân. Tính chiều cao của thùng phi được làm. A. 15/4(cm) B. 5(cm) C. 15/2(cm) D. 15(cm)
Đọc tiếp
Để làm một thùng phi hình trụ người ta cần hai miếng nhựa hình tròn làm hai đáy có diện tích mỗi hình là 4π(c m 2 ) và một miếng nhựa hình chữ nhật có diện tích là 15π(c m 2 ) để làm thân. Tính chiều cao của thùng phi được làm.
A. 15/4(cm)
B. 5(cm)
C. 15/2(cm)
D. 15(cm)
Cần phải thiết kế các thùng dạng hình trụ có nắp đựng nước sạch có dung tích V (
c
m
3
). Hỏi bán kính R (cm) của đáy hình trụ nhận giá trị nào sau đây để tiết kiệm vật liệu nhất?
Đọc tiếp
Cần phải thiết kế các thùng dạng hình trụ có nắp đựng nước sạch có dung tích V ( c m 3 ). Hỏi bán kính R (cm) của đáy hình trụ nhận giá trị nào sau đây để tiết kiệm vật liệu nhất?
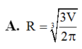
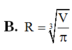
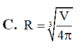
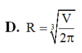
Một thùng chứa không nắp có thê tích 10 m3 với đáy hinh chữ nhật có chiều dài gấp đôi chiều rộng. Biết vật liệu làm đáy thùng có giá $10/m2 và làm thành thùng có giá $6/m2. Tìm các cạnh (dài, rộng, cao) của thùng sao cho chi phí là tối thiều.
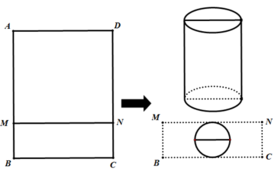
Sử dụng mảnh inox hình chữ nhật ABCD có diện tích bằng
1
m
2
và cạnh BC x (m) để làm một thùng đựng nước có đáy, không có nắp theo quy trình như sau: Chia hình chữ nhật ABCD thành 2 hình chữ nhật ADNM và BCNM, trong đó phần hình chữ nhật ADNM được gò thành phần xung quanh hình trụ có chiều cao bằng AM; phần hình chữ nhật BCNM được cắt ra một hình tròn để làm đáy của hình trụ trên (phần inox còn thừa được bỏ đi). Tính gần đúng giá trị x để thùn...
Đọc tiếp
Sử dụng mảnh inox hình chữ nhật ABCD có diện tích bằng 1 m 2 và cạnh BC= x (m) để làm một thùng đựng nước có đáy, không có nắp theo quy trình như sau: Chia hình chữ nhật ABCD thành 2 hình chữ nhật ADNM và BCNM, trong đó phần hình chữ nhật ADNM được gò thành phần xung quanh hình trụ có chiều cao bằng AM; phần hình chữ nhật BCNM được cắt ra một hình tròn để làm đáy của hình trụ trên (phần inox còn thừa được bỏ đi). Tính gần đúng giá trị x để thùng nước trên có thể tích lớn nhất (coi như các mép nối không đáng kể).
![]()
![]()
![]()
Một nhà sản xuất cần thiết kế một thùng sơn dạng hình trụ có nắp đậy với dug tích là 20 lít. Cần phải thiết kế thùng sơn đó với bán kính nắp đậy là bao nhiêu (cm) để nhà sản xuất tiết kiệm được vật liệu nhất?
Đọc tiếp
Một nhà sản xuất cần thiết kế một thùng sơn dạng hình trụ có nắp đậy với dug tích là 20 lít. Cần phải thiết kế thùng sơn đó với bán kính nắp đậy là bao nhiêu (cm) để nhà sản xuất tiết kiệm được vật liệu nhất?
![]()
![]()
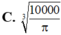
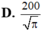
Từ một tấm tôn có kích thước 1m x 2m, người ta làm ra chiếc thùng đựng nước theo hai cách (xem hình minh họa dưới đây) – Cách 1: làm ra thùng hình trụ có chiều cao 1m, bằng cách gò tấm tôn ban đầu thành mặt xung quanh của thùng. – Cách 2: làm ra thùng hình hộp chữ nhật có chiều cao 1m, bằng cách chia tấm tôn ra thành 4 phần rồi gò thành các mặt bên của hình hộp chữ nhật. Kí hiệu
V
1
là thể tích của thùng được gò theo cách 1 và
V...
Đọc tiếp
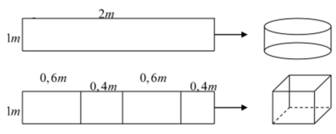
Từ một tấm tôn có kích thước 1m x 2m, người ta làm ra chiếc thùng đựng nước theo hai cách (xem hình minh họa dưới đây)
– Cách 1: làm ra thùng hình trụ có chiều cao 1m, bằng cách gò tấm tôn ban đầu thành mặt xung quanh của thùng.
– Cách 2: làm ra thùng hình hộp chữ nhật có chiều cao 1m, bằng cách chia tấm tôn ra thành 4 phần rồi gò thành các mặt bên của hình hộp chữ nhật.
Kí hiệu V 1 là thể tích của thùng được gò theo cách 1 và V 2 là thể tích của thùng được gò theo cách 2. Tính tỷ số V 1 V 2 .