\(\left(A+B\right)^2=A^2+2AB+B^2\)
\(\left(A-B\right)^2=A^2-2AB+B^2\)
\(A^2-B^2=\left(A-B\right)\left(A+B\right)\)
\(A^3+B^3=\left(A+B\right)\left(A^2-AB+B^2\right)\)
\(A^3-B^3=\left(A-B\right)\left(A^2+AB+B^2\right)\)
\(\left(A+B\right)^3=A^3+3A^2B+3AB^2+B^3\)
\(\left(A-B\right)^3=A^3-3A^2B+3AB^2-B^3\)
* Bình phương của 1 tổng:
\(\left(A+B\right)^2=A^2+2AB+B^2\)
* Bình phương của 1 hiệu :
\(\left(A-B\right)^2=A^2-2AB+B^2\)
* Hiệu 2 bình phương :
\(A^2-B^2=\left(A+B\right)\left(A-B\right)\)
* Lập phương của một tổng :
\(\left(A+B\right)^3=A^3+2.A^2B+2.AB^2+B^3\)
* Lập phương của một hiệu:
\(\left(A-B\right)^3=A^3-2A^2B+2AB^2-B^3\)
* Tổng hai lập phương :
\(A^3+B^3=\left(A+B\right)\left(A^2-AB+B^2\right)\)
* Hiệu hai lập phương :
\(A^3-B^3=\left(A-B\right)\left(A^2+AB+B^2\right)\)
1. (A+B)2 = A2+2AB+B2
2. (A – B)2= A2 – 2AB+ B2
3. A2 – B2= (A-B)(A+B)
4. (A+B)3= A3+3A2B +3AB2+B3
5. (A – B)3 = A3- 3A2B+ 3AB2- B3
6. A3 + B3= (A+B)(A2- AB +B2)
7. A3- B3= (A- B)(A2+ AB+ B2)
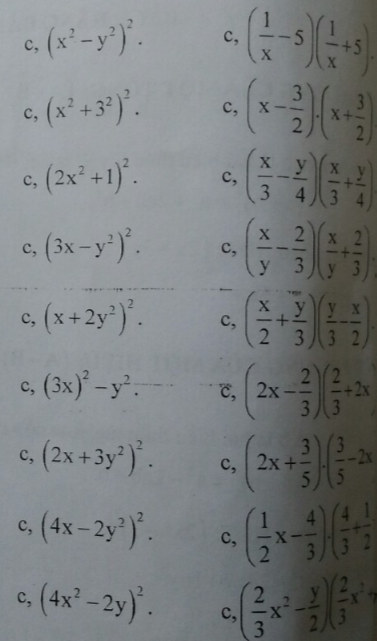viết lại các đa thức thành các vế kia hằng đẳng thức giúp em với ạ em đang cần gấp 
