Các câu hỏi tương tự
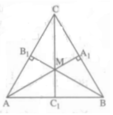
Cho tam giác ABC cân tại C. Kẻ các đường cao AA1 và BB1 của tam giác đó. Hai đường cao này cắt nhau tại M. Chứng minh rằng đường thẳng MC là đường trung trực của đoạn thẳng AB.
Cho tam giác ABC có các đường trung tuyến AM, BN, CP trọng tâm G. Gọi K là trung điểm của GB
Chứng minh rằng các cạnh của tam giác GMK bằng 1/3 các trung tuyến tam giác ABC
Nêu cách dựng tam giac ABC khi biết đọ dài 3 đường trung tuyến AM, BN, CP
Cho tam giác ABC nội tiếp đường tròn(O), I là trung đieerm BC,M là đieerm trên đoạn CI(M khác C, I). Đường thẳng AM cắt đường tròn (O) tại D. Tiếp tuyến của đường tròn ngoại tiếp tam giác AMI tại M cắt các đoajn thẳng BD,DC lần lượt tại P và Q. Chứng minh M là trung đieerm PQ
Cho tam giác ABC cân tại A trung tuyến AM. Qua điểm B vẽ đường thẳng song song AC cắt đường thẳng AM tại D
a, C/m tam giác AMC = tam giác DMB
b, C/m AB = BD
c, Gọi P là trung điểm đoạn thẳng AB, đoạn thẳng PD cắt đoạn thẳng PC tại O. Trên tia đối tia PC lấy điểm N sao cho PN = PO. C/m O là trọng tâm tam giác ABD và NA = 2 lần OM
Cho tam giác ABC cân tại A, AM là đường trung tuyến.
a) Cho biết AB = AC = 13cm, BC = 10cm. Tính AM.
b) Vẽ AN là đường trung tuyến của tam giác ABM. Gọi N là trung điểm của đoạn thẳng AD, E là trung điểm của đoạn thẳng CD. Chứng minh rằng A, M, E thẳng hàng.
Cho tam giác ABC đường trung tuyến AM từ M kẻ đường thẳng song song với AB cắt AC tại M biết AM = NM . BN cắt AM ở đỉnh O . C/M
a) tam giác ABC là tam giác cân và AM là đường trung trực của đoạn thẳng BC
b) N là trung điểm của AC
c) gọi k là trung điểm của AB . C/M 3 điểm C, O, K thẳng hàng
1 Nêu tính chất 3 đường trung tuyến , tia phân giác của một góc , đường phân giác của tam giác
2 Nêu cách chứng minh 3 điểm thẳng hàng
1. cho tam giác ABC vẽ 3 đường trung tuyến, 3 đường phân giác và nêu tính chất của chúng
2 cho tam giác ABC vẽ 3 đường trung trực, 3 đường cao và nêu tính chất của chúng
Cho tam giác MNP cân tại M với các đường trung tuyến NA, PB và trọng tâm G. Trên nửa mặt phẳng không chứa M, vẽ đoạn thẳng NC song song và bằng PB. Chứng minh :
a, Tam giác NAC là tam giác cân
b, NP là đường trung trực của đoạn thẳng AC










