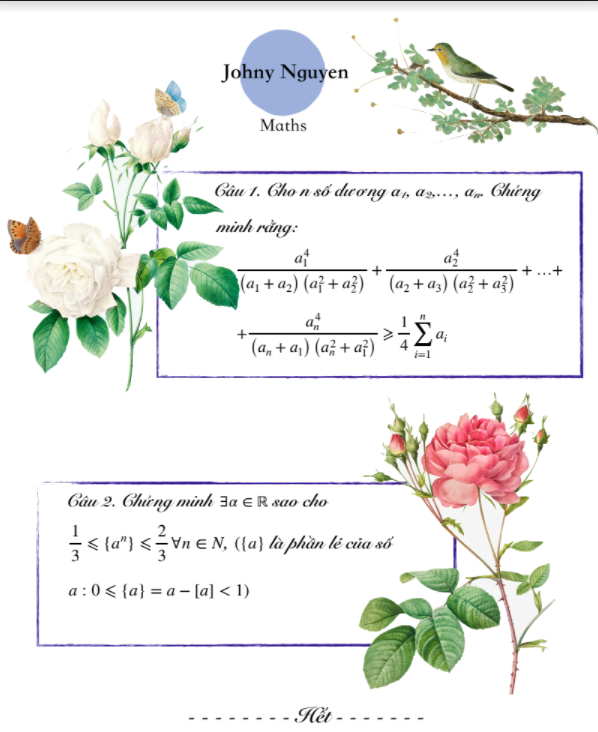
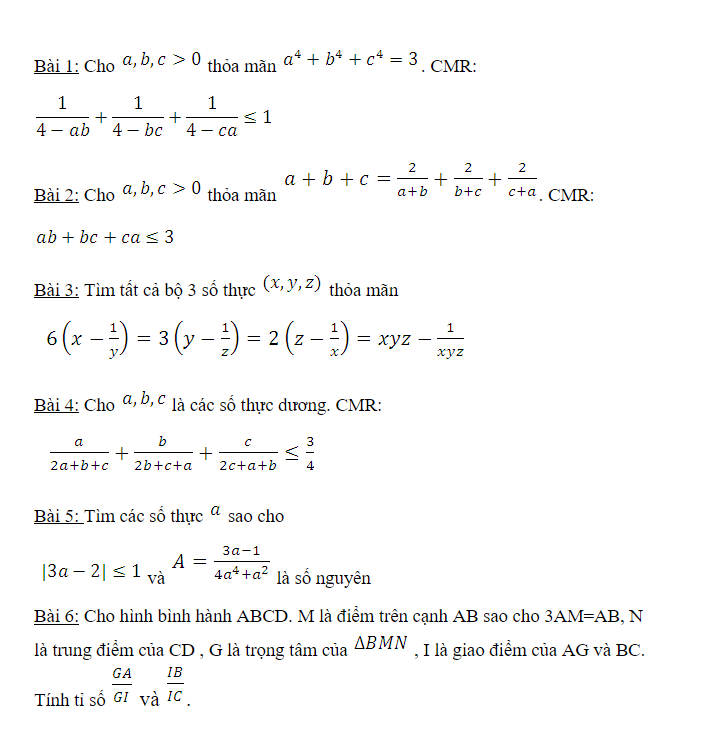Muốn câu hỏi mình xuất hiện trong chuyên mục? Gửi ngay câu hỏi tới: https://forms.gle/PBruN2d3LXicucxu6. Chúng mình sẽ duyệt những câu hỏi hay nhất!
Hãy tương tác với page Facebook nữa nha! Cuộc thi Trí tuệ VICE | Facebook
(2-4 điểm thưởng/1 ý làm)
| Toán.C24 _ 3.8.2021 | Phạm Nguyễn Hồng Anh (Hoc24) |
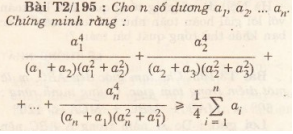
| Toán.C25 _ 3.8.2021 | Trần Thanh Phương (Hoc24) |
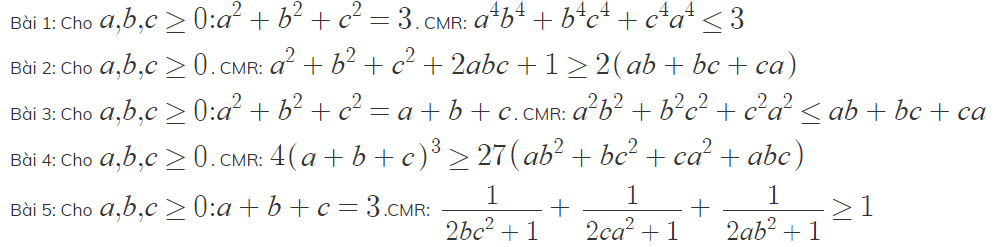
Bài 2.
Ta có:a2+b2+c2+2abc+1≥2(ab+bc+ca)
⇔ (a2-2ab+b2)+(c2-2c+1)+(2c+2abc-2bc-2ca)≥0
⇔ (a-b)2+(c-1)2+2c(a-1)(b-1)≥0
Vì a,b,c≥0 ⇒ 2c(a-1)(b-1)≥0
Dấu "=" xảy ra ⇔ a=b=c=1
C25: b5: Sử dụng kĩ thuật Côsi ngược dấu:
Ta có: \(\dfrac{1}{2bc^2+1}=1-\dfrac{2bc^2}{2bc^2+1}\ge1-\dfrac{2bc^2}{3\sqrt[3]{b^2c^4}}=1-\dfrac{2\sqrt[3]{bc^2}}{3}\)
Cmtt ta được: \(\dfrac{1}{2ca^2+1}\ge1-\dfrac{2\sqrt[3]{ca^2}}{3};\dfrac{1}{2ab^2+1}\ge1-\dfrac{2\sqrt[3]{ab^2}}{3}\)
\(\Rightarrow VT\ge1-\dfrac{2\sqrt[3]{bc^2}}{3}+1-\dfrac{2\sqrt[3]{ca^2}}{3}+1-\dfrac{2\sqrt[3]{ab^2}}{3}=3-2\left(\dfrac{\sqrt[3]{bc^2}+\sqrt[3]{ca^2}+\sqrt[3]{ab^2}}{3}\right)\)
Ta có: Theo bđt Côsi:
\(\sqrt[3]{bc^2}=\sqrt[3]{b.c.c}\le\dfrac{b+c+c}{3}=\dfrac{b+2c}{3}\)
\(\sqrt[3]{ca^2}=\sqrt[3]{c.a.a}\le\dfrac{c+a+a}{3}=\dfrac{c+2a}{3}\)
\(\sqrt[3]{ab^2}=\sqrt[3]{a.b.b}\le\dfrac{a+b+c}{3}=\dfrac{a+2b}{3}\)
\(\Rightarrow\sqrt[3]{bc^2}+\sqrt[3]{ca^2}+\sqrt[3]{ab^2}\le\dfrac{b+2c+c+2a+a+2b}{3}=a+b+c=3\)
\(\Rightarrow3-2\left(\dfrac{\sqrt[3]{bc^2}+\sqrt[3]{ca^2}+\sqrt[3]{ab^2}}{3}\right)=1\)
\(\Rightarrow VT\ge1\)
Dấu ''='' xảy ra khi a=b=c=1
bài 4
\(VT\ge VP=>VT-VP\ge0\)
mà \(VT\ge4\left(3\sqrt[3]{abc}\right)^3=4.27abc=>VT-4.27abc\ge0\)
nên ta cần chứng minh \(VP=4.27abc\)
\(=>ab^2+bc^2+ca^2+abc=4.abc\)
\(< =>ab^2+bc^2+ca^2=3abc\)(1)
có \(ab^2+bc^2+ca^2\ge3abc\) dấu"=" xảy ra tại a=b=c
thì (1) đúng \(=>VT\ge VP\) khi a=b=c
(cách này ko biết đúng khum=))
Toán C25, bài 1) đề sai. Thử a=1; b=1/2; c= sqrt(7)/2 là sẽ thấy.
Như mấy bạn kia nói, đúng là câu \(25.1\) đề không chính xác
Cách chứng minh khá đơn giản:
Đặt \(\left(a^2;b^2;c^2\right)=\left(x;y;z\right)\)
Ta có:
\(81=\left(x+y+z\right)^4=\left(x^2+y^2+z^2+2\left(xy+yz+zx\right)\right)^2\ge8\left(x^2+y^2+z^2\right)\left(xy+yz+zx\right)\)
\(=8\left[xy\left(x^2+y^2\right)+yz\left(y^2+z^2\right)+zx\left(z^2+x^2\right)+xyz\left(x+y+z\right)\right]\)
\(\ge8\left[xy\left(x^2+y^2\right)+yz\left(y^2+z^2\right)+zx\left(x^2+z^2\right)\right]\)
\(\ge8\left(xy.2xy+yz.2yz+zx.2zx\right)=16\left(x^2y^2+y^2z^2+z^2x^2\right)\)
\(\Rightarrow x^2y^2+y^2z^2+z^2x^2\le\dfrac{81}{16}\)
Toán C25, bài 1): Để đề đúng thì phải sửa giả thiết thành: \(a^3 +b^3 +c^3 =3\)
Toán C25, bài 1): Để đề đúng thì phải sửa giả thiết thành: a3+b3+c3=3















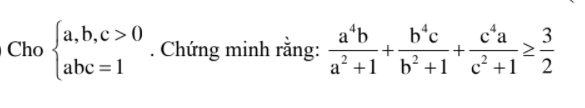
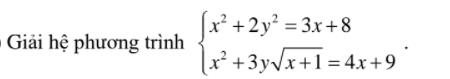
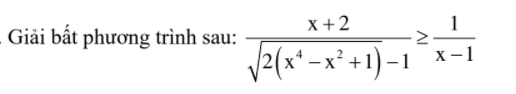
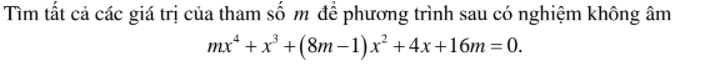

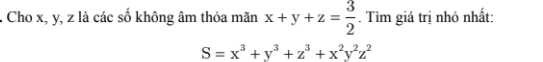
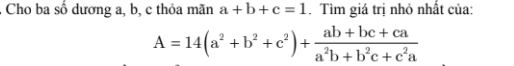
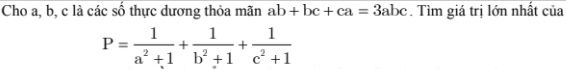
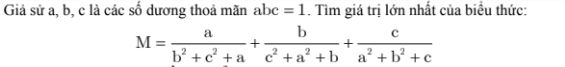




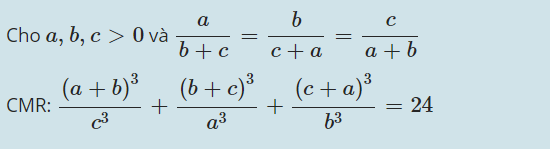
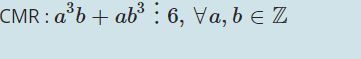
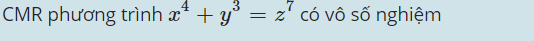

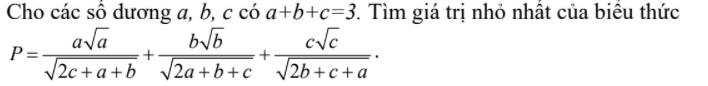

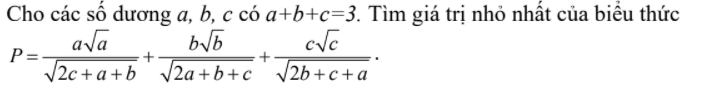
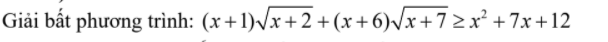

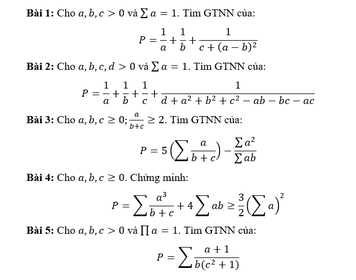



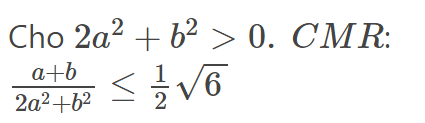
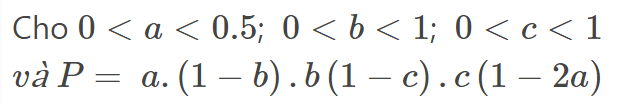
 4)
4)