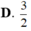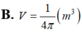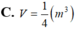Các câu hỏi tương tự
Người ta gỡ các mặt của một hình hộp chữ nhật bằng tôn có kích thước 1m × 2m × 3m để quây xung quanh một bể chứa hình trụ có chiều cao 1mét và vừa hết số tôn. Hỏi thể tích của bể chứa đó là bao nhiêu mét khối? A.
V
9
π
B.
V
9
π
2
C.
V
9
π
D.
V...
Đọc tiếp
Người ta gỡ các mặt của một hình hộp chữ nhật bằng tôn có kích thước 1m × 2m × 3m để quây xung quanh một bể chứa hình trụ có chiều cao 1mét và vừa hết số tôn. Hỏi thể tích của bể chứa đó là bao nhiêu mét khối?
A. V = 9 π
B. V = 9 π 2
C. V = 9 π
D. V = 128 π
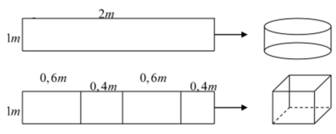
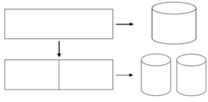
Từ một tấm tôn có kích thước 1m x 2m, người ta làm ra chiếc thùng đựng nước theo hai cách (xem hình minh họa dưới đây) – Cách 1: làm ra thùng hình trụ có chiều cao 1m, bằng cách gò tấm tôn ban đầu thành mặt xung quanh của thùng. – Cách 2: làm ra thùng hình hộp chữ nhật có chiều cao 1m, bằng cách chia tấm tôn ra thành 4 phần rồi gò thành các mặt bên của hình hộp chữ nhật. Kí hiệu
V
1
là thể tích của thùng được gò theo cách 1 và
V...
Đọc tiếp
Từ một tấm tôn có kích thước 1m x 2m, người ta làm ra chiếc thùng đựng nước theo hai cách (xem hình minh họa dưới đây)
– Cách 1: làm ra thùng hình trụ có chiều cao 1m, bằng cách gò tấm tôn ban đầu thành mặt xung quanh của thùng.
– Cách 2: làm ra thùng hình hộp chữ nhật có chiều cao 1m, bằng cách chia tấm tôn ra thành 4 phần rồi gò thành các mặt bên của hình hộp chữ nhật.
Kí hiệu V 1 là thể tích của thùng được gò theo cách 1 và V 2 là thể tích của thùng được gò theo cách 2. Tính tỷ số V 1 V 2 .
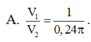
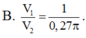
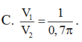
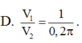
Một chiếc hộp tôn có 6 mặt là các tấm tôn hình vuông có cạnh bằng 1 mét. Người ta gỡ các tấm tôn của chiếc hộp đó và quây thành mặt xung quanh của một hình trụ thì diện tích đáy S của hình trụ đó bằng bao nhiêu (chiều cao hình trụ là 1 mét).
Đọc tiếp
Một chiếc hộp tôn có 6 mặt là các tấm tôn hình vuông có cạnh bằng 1 mét. Người ta gỡ các tấm tôn của chiếc hộp đó và quây thành mặt xung quanh của một hình trụ thì diện tích đáy S của hình trụ đó bằng bao nhiêu (chiều cao hình trụ là 1 mét).
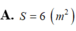
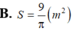
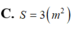
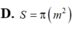
Từ một tấm tôn hình chữ nhật kích thước
50
c
m
x
240
c
m
,
người ta làm các thùng đựng nước hình trụ có chiều cao bằng 50cm, theo hai cách sau (xem hình minh họa dưới đây):- Cách 1: Gò tấm tôn ban đầu thành mặt xung quanh của thùng- Cách 2: Cắt tấm tôn ban đầu thành hai tấm bằng nhau, rồi gò mỗi tấm đó thành mặt xung quanh của một thùng.Kí hiệu
V
1
là thể tích...
Đọc tiếp
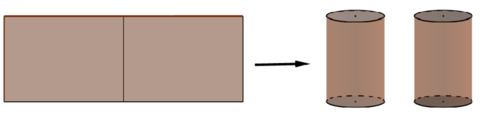
Từ một tấm tôn hình chữ nhật kích thước 50 c m x 240 c m , người ta làm các thùng đựng nước hình trụ có chiều cao bằng 50cm, theo hai cách sau (xem hình minh họa dưới đây):
- Cách 1: Gò tấm tôn ban đầu thành mặt xung quanh của thùng
- Cách 2: Cắt tấm tôn ban đầu thành hai tấm bằng nhau, rồi gò mỗi tấm đó thành mặt xung quanh của một thùng.
Kí hiệu V 1 là thể tích của thùng được theo cách 1 và V 2 là tổng thể tích của hai thùng được theo cách 2. Tính tỉ số V 1 V 2
A. V 1 V 2 = 1
B. V 1 V 2 = 2
C. V 1 V 2 = 1 2
D. V 1 V 2 = 4
Từ một tấm tôn hình chữ nhật có kích thước 5mx40m, người ta làm hai thùng nước hình trụ có cùng chiều cao 5m, bằng cách cắt tấm tôn đó thành hai tấm bằng nhau, rồi gò mỗi tấm đó thành mặt xung quanh của một thùng (tham khảo hình bên dưới). Tổng thể tích của hai cái thùng hình trụ bằng
Đọc tiếp
Từ một tấm tôn hình chữ nhật có kích thước 5mx40m, người ta làm hai thùng nước hình trụ có cùng chiều cao 5m, bằng cách cắt tấm tôn đó thành hai tấm bằng nhau, rồi gò mỗi tấm đó thành mặt xung quanh của một thùng (tham khảo hình bên dưới).
Tổng thể tích của hai cái thùng hình trụ bằng
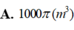
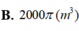
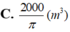
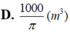
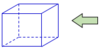
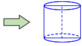
Cho hai tấm tôn hình chữ nhật đều có kích thước 1,5mx8m. Tấm tôn thứ nhất được chế tạo thành một hình hộp chữ nhật không đáy, không nắp, có thiết diện ngang là một hình vuông (mặt phẳng vuông góc với đường cao của hình hộp và cắt các mặt bên của hình hộp theo các đoạn giao tuyến tạo thành một hình vuông) và có chiều cao 1,5m, còn tấm tôn thứ hai được chế tạo thành một hình trụ không đáy, không nắp và cũng có chiều cao 1,5m. Gọi
V
1
,
V...
Đọc tiếp
Cho hai tấm tôn hình chữ nhật đều có kích thước 1,5mx8m. Tấm tôn thứ nhất được chế tạo thành một hình hộp chữ nhật không đáy, không nắp, có thiết diện ngang là một hình vuông (mặt phẳng vuông góc với đường cao của hình hộp và cắt các mặt bên của hình hộp theo các đoạn giao tuyến tạo thành một hình vuông) và có chiều cao 1,5m, còn tấm tôn thứ hai được chế tạo thành một hình trụ không đáy, không nắp và cũng có chiều cao 1,5m. Gọi
V
1
,
V
2
, theo thứ tự là thể tích của khối hộp chữ nhật và thể tích của khối trụ. Tính tỉ số
V
1
V
2
.

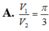
![]()
![]()
![]()
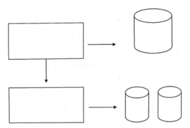
Từ một tấm tôn hình chữ nhật kích thước 80cmx360cm, người ta làm các thùng đựng nước hình trụ có chiều cao bằng 80cm, theo hai cách sau (xem hình minh họa dưới đây): * Cách 1: Gò tấm tôn ban đầu thành mặt xung quanh của thùng. * Cách 2: Cắt tấm tôn ban đầu thành hai tấm bằng nhau, rồi gò mỗi tấm đó thành mặt xung quanh của một thùng.Kí hiệu
V
1
là thể tích của thùng gò được theo cách 1 và
V
2
là tổng thể tí...
Đọc tiếp
Từ một tấm tôn hình chữ nhật kích thước 80cmx360cm, người ta làm các thùng đựng nước hình trụ có chiều cao bằng 80cm, theo hai cách sau (xem hình minh họa dưới đây):
* Cách 1: Gò tấm tôn ban đầu thành mặt xung quanh của thùng.
* Cách 2: Cắt tấm tôn ban đầu thành hai tấm bằng nhau, rồi gò mỗi tấm đó thành mặt xung quanh của một thùng.Kí hiệu
V
1
là thể tích của thùng gò được theo cách 1 và
V
2
là tổng thể tích của hai thùng gò được theo cách 2. Tính tỉ số
V
1
V
2
.
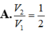

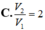
![]()
Từ một tấm tôn hình chữ nhật kích thước 50cm
×
240cm người ta làm các thùng đựng nước hình trụ có chiều cao bằng 50cm, theo hai cách sau (xem hình minh họa dưới đây) * Cách 1: Gò tấm tôn ban đầu thành mặt xung quanh của thùng. * Cách 2: Cắt tấm tôn ban đầu thành hai tấm tôn bằng nhau, rồi gò mỗi tấm đó thành mặt xung quanh của một thùng. Kí hiệu
V
1
là thể tích của thùng gò được theo cách 1 và
V
2...
Đọc tiếp
Từ một tấm tôn hình chữ nhật kích thước 50cm × 240cm người ta làm các thùng đựng nước hình trụ có chiều cao bằng 50cm, theo hai cách sau (xem hình minh họa dưới đây)
* Cách 1: Gò tấm tôn ban đầu thành mặt xung quanh của thùng.
* Cách 2: Cắt tấm tôn ban đầu thành hai tấm tôn bằng nhau, rồi gò mỗi tấm đó thành mặt xung quanh của một thùng.
Kí hiệu V 1 là thể tích của thùng gò được theo cách 1 và V 2 là tổng thể tích của hai thùng gò được theo cách 2. Tính tỉ số V 1 V 2 .
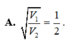
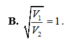
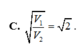
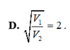
Cho tam giác ABC vuông tại A. Đường thẳng d đi qua A và song song với BC. Cạnh BC quay xung quanh d tạo thành một mặt xung quanh của hình trụ có thể tích là V1. Tam giác ABC quay xung quanh trục d được khối tròn xoay có thể tích là V2. Tính tỉ số
V
1
V
2
.
Đọc tiếp
Cho tam giác ABC vuông tại A. Đường thẳng d đi qua A và song song với BC. Cạnh BC quay xung quanh d tạo thành một mặt xung quanh của hình trụ có thể tích là V1. Tam giác ABC quay xung quanh trục d được khối tròn xoay có thể tích là V2. Tính tỉ số V 1 V 2 .
![]()
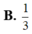
![]()