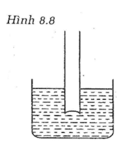
Một ống thủy tinh hở hai đầu có chiều dài l =50cm và tiết diện S = 2cm2 được cằm vuông góc vào một chậu nước . Rót 40g dầu ( có trọng lượng riêng bằng d = 8000 N / m3 ) vào ống. a ) Xác định độ chênh lệch giữa mức dầu trong ống và mức nước trong chậu b ) Phải đặt đầu trên của ống cách mặt nước khoảng bằng bao nhiêu để có thể rót dầu vào đầy ống . c ) Xác định lượng dầu chảy ra ngoài khi ống đang ở vị trí của câu b ) được kéo lên một đoạn 2cm ( hoặc 1 đoạn x ) .
a, thể tích của dầu là : Vd = \(\dfrac{m_d}{D_d}\) = \(\dfrac{0,04}{800}\) = 5.10-5 (m3)
chiều cao của cột dầu là : hd = \(\dfrac{V_d}{S}\) = \(\dfrac{5.10^{-5}}{0,0002}\) = 0,25 (m)
xét điểm A nằm trên cùng mặt phân cách giữa nước và dầu và điểm B nằm trên cùng mặt phân cách ở ngoài ống thủy tinh
ta có : PA = PB
<=> dd . hd = dnước . h2 ( h2 là độ cao mực dầu trong chậu nước )
<=> 8000.0,25 = 10000. h2
<=> h2 = 0,2 m
=> h = hd - h2 = 0,25 - 0,2 = 0,05 m
độ chênh lệch hai mặt thoáng là 0,05m
b, xét điểm A nằm trên mặt phân cách gữa nước và dầu và điểm B cùng mặt phân cách ở ngoài ống
PA = PB
=> dd . h = dnước . h3
=> 8000.0,5 = 10000. h3
=> h3 = 0,4 m
vậy phải đặt ống cách mặt thoáng 0,4m để có thể rót dầu vào đầy ống
=> miệng ống cách mặt nước 0,5-0,4=0,1m
c, khi kéo ống lên 1 đoạn 2cm = 0,002m, một phần dầu bị chảy ra ngoài và khi đã ổn định chiều cao cột dầu còn lại trong ống là l1 , ta có :
Pc = dd.l1 = dnước.( l - y-2 )
=> l1 = \(\dfrac{d_{nước}}{d_d}\) . ( 0,4-0,002) = \(\dfrac{10000}{8000}\) . 0,38 = 0,475 (m)
tương tự với kéo lên một đoạn là x , ta có :
=> l1 = \(\dfrac{d_{nước}}{d_d}\) . ( 0,4 - x ) = \(\dfrac{10000}{8000}\) . (0,4-x)
vậy ....