Các câu hỏi tương tự
Một khinh khí cầu có một mặt cầu có đường kính 11m. Nếu làm tròn kết quả đến chữ số thập phân thứ hai, thì diện tích bề mặt khinh khí cầu là:A. 379,94 (
m
2
) B. 697,19 (
m
2
)C. 190,14 (
m
2
) D. 95,07 (
m
2
)
Đọc tiếp
Một khinh khí cầu có một mặt cầu có đường kính 11m. Nếu làm tròn kết quả đến chữ số thập phân thứ hai, thì diện tích bề mặt khinh khí cầu là:
A. 379,94 ( m 2 ) B. 697,19 ( m 2 )
C. 190,14 ( m 2 ) D. 95,07 ( m 2 )
I. Trắc nghiệm ( 6 điểm)Một mặt cầu có đường kính 11m thì diện tích của mặt cầu là bao nhiêu? (lấy
π
≈
22
7
và làm tròn kết quả đến chữ số thập phân thứ hai). A. 379,94
m
2
B. 697,19
m
2
C. 190,14
m
2
D. 380,29
m
2
Đọc tiếp
I. Trắc nghiệm ( 6 điểm)
Một mặt cầu có đường kính 11m thì diện tích của mặt cầu là bao nhiêu? (lấy π ≈ 22 7 và làm tròn kết quả đến chữ số thập phân thứ hai).
A. 379,94 m 2
B. 697,19 m 2
C. 190,14 m 2
D. 380,29 m 2
Cho mặt cầu (S) có bán kính R 5 (cm). Mặt phẳng (P) cắt mặt cầu (S) theo giao tuyến là đường tròn (C) có chu vi bằng 8
π
(cm). Bốn điểm A, B, C, D thay đổi sao cho A, B, C thuộc đường tròn (C), điểm D thuộc (S) (D không thuộc đường tròn (C)) và tam giác ABC là tam giác đều. Thể tích lớn nhất của khối tự diện ABCD bằng bao nhiêu? A. 32
3
(
c
m
3
) B. 60
3...
Đọc tiếp
Cho mặt cầu (S) có bán kính R = 5 (cm). Mặt phẳng (P) cắt mặt cầu (S) theo giao tuyến là đường tròn (C) có chu vi bằng 8 π (cm). Bốn điểm A, B, C, D thay đổi sao cho A, B, C thuộc đường tròn (C), điểm D thuộc (S) (D không thuộc đường tròn (C)) và tam giác ABC là tam giác đều. Thể tích lớn nhất của khối tự diện ABCD bằng bao nhiêu?
A. 32 3 ( c m 3 )
B. 60 3 ( c m 3 )
C. 20 3 ( c m 3 )
D. 96 3 ( c m 3 )
Một chậu nước hình bán cầu bằng nhôm có bán kính R10(cm). Trong chậu có chứa sẵn mọt khối nước hình chõm cầu có chiều cao h4(cm). Người ta bỏ vào chậu một viên bi hình cầu bằng kim loại thì mặt nước dâng lên vừa phủ kín viên bi. Tính bán kinh của viên bi (kết quả làm tròn đến 2 chữ số lẻ thập phân).
Đọc tiếp
Một chậu nước hình bán cầu bằng nhôm có bán kính R=10(cm). Trong chậu có chứa sẵn mọt khối nước hình chõm cầu có chiều cao h=4(cm). Người ta bỏ vào chậu một viên bi hình cầu bằng kim loại thì mặt nước dâng lên vừa phủ kín viên bi. Tính bán kinh của viên bi (kết quả làm tròn đến 2 chữ số lẻ thập phân).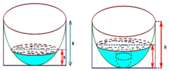
![]()
![]()
![]()
![]()
Trong không gian Oxyz, cho mặt cầu (S):
x
-
1
2
+
y
-
2
2
+
z
-
3
2
25
và hai điểm A(3;-2;6) và B(0;1;0). Mặt phẳng (P):ã+by+cz-20 chứa đường thẳ...
Đọc tiếp
Trong không gian Oxyz, cho mặt cầu (S): x - 1 2 + y - 2 2 + z - 3 2 = 25 và hai điểm A(3;-2;6) và B(0;1;0). Mặt phẳng (P):ã+by+cz-2=0 chứa đường thẳng AB và cắt (S) theo giao tuyến là đường tròn có bán kính nhỏ nhất. Tính giá trị của biểu thức M = 2a + b – c.
A. M = 2
B. M = 3
C. M = 1
D. M = 4
Một người thợ có một khối đá hình trụ. Kẻ hai đường kính MN, PQ của hai đáy sao cho MN
⊥
PQ. Người thợ đó cắt khối đá theo các mặt cắt đi qua 3 trong 4 điểm M, N, P, Q để thu được một khối đá có hình tứ diện MNPQ. Biết rằng MN 60 cm và thể tích của khối tứ diện MNPQ bằng
30
d
m
3
. Hãy tính thể tích của lượng đá bị cắt bỏ (làm tròn kết quả đến 1 chữ số thập phân)
Đọc tiếp
Một người thợ có một khối đá hình trụ. Kẻ hai đường kính MN, PQ của hai đáy sao cho MN ⊥ PQ. Người thợ đó cắt khối đá theo các mặt cắt đi qua 3 trong 4 điểm M, N, P, Q để thu được một khối đá có hình tứ diện MNPQ. Biết rằng MN = 60 cm và thể tích của khối tứ diện MNPQ bằng 30 d m 3 . Hãy tính thể tích của lượng đá bị cắt bỏ (làm tròn kết quả đến 1 chữ số thập phân)
![]()
![]()
![]()
![]()
Một hình hộp chữ nhật có ba kích thước lần lượt là a, b, c. Gọi (S) là mặt cầu đi qua 8 đỉnh của hình hộp chữ nhật đó. Diện tích của mặt cầu (S) theo a, b, c là:A.
π
(
a
2
+
b
2
+
c
2
) B. 2
π
(
a...
Đọc tiếp
Một hình hộp chữ nhật có ba kích thước lần lượt là a, b, c. Gọi (S) là mặt cầu đi qua 8 đỉnh của hình hộp chữ nhật đó. Diện tích của mặt cầu (S) theo a, b, c là:
A. π ( a 2 + b 2 + c 2 ) B. 2 π ( a 2 + b 2 + c 2 )
C. 4 π ( a 2 + b 2 + c 2 ) D. π /2.( a 2 + b 2 + c 2 )
Trong không gian Oxyz, cho mặt cầu
(
S
)
:
x
+
1
2
+
y
+
2
2
+
z
2...
Đọc tiếp
Trong không gian Oxyz, cho mặt cầu ( S ) : x + 1 2 + y + 2 2 + z 2 = 4 và các điểm A(-2;0;-2 2 ), B(-4;-4;0). Biết rằng tập hợp các điểm M thuộc (S) và thỏa mãn M A 2 + M O → . M B → = 16 là một đường tròn. Tính bán kính đường tròn đó.
A. 3 2 4 .
B. 3 2 .
C. 3 7 4 .
D. 5 2 .
Trong không gian Oxyz, cho mặt cầu
S
:
x
2
+
y
2
+
x
+
2
2
16
và điểm A(m;m;2) nằm ngoài mặt cầu. Từ A kẻ các tiếp tuyến đến mặt cầu (S), gọi
P
m
là mặt phẳng chứa các tiếp điểm, biết ...
Đọc tiếp
Trong không gian Oxyz, cho mặt cầu S : x 2 + y 2 + x + 2 2 = 16 và điểm A(m;m;2) nằm ngoài mặt cầu. Từ A kẻ các tiếp tuyến đến mặt cầu (S), gọi P m là mặt phẳng chứa các tiếp điểm, biết P m luôn đi qua một đường thẳng d cố định, phương trình đường thẳng d là:
A. 
B. 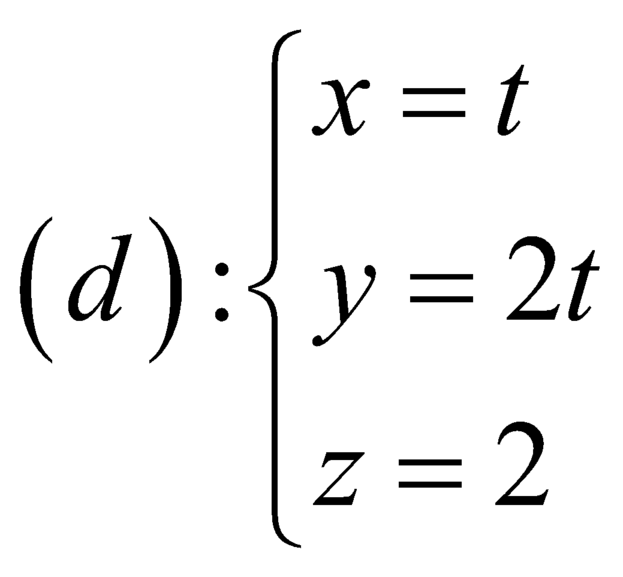
C. 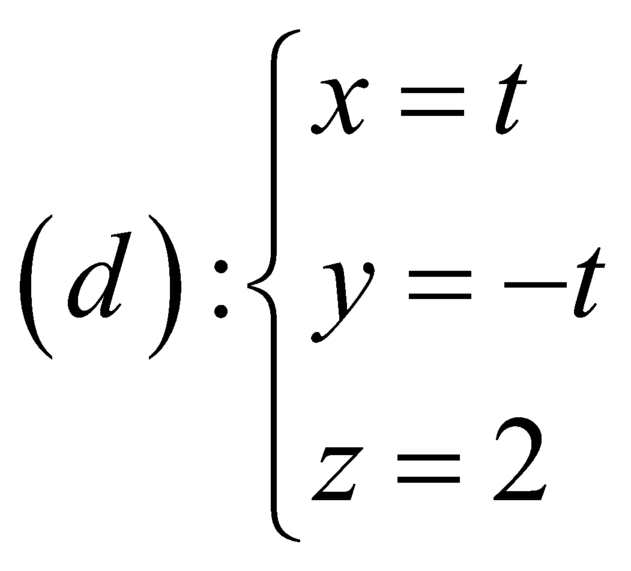
D. 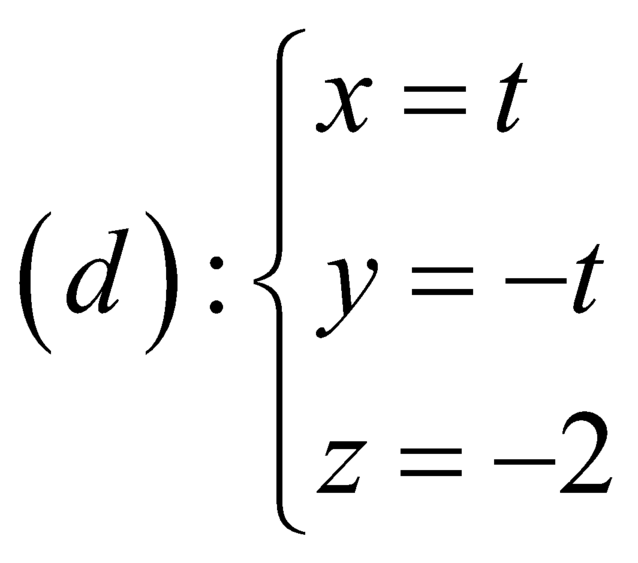 .
.



