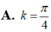Các câu hỏi tương tự
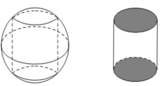
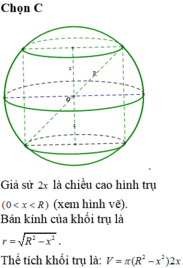
Một khối đá có hình là một khối cầu có bán kính R, người thợ thợ thủ công mỹ nghệ cần cắt và gọt viên đá đó thành một viên đá cảnh có hình dạng là một khối trụ. Tính thể tích lớn nhất có thể của viên đá cảnh sau khi đã hoàn thiện.
Đọc tiếp
Một khối đá có hình là một khối cầu có bán kính R, người thợ thợ thủ công mỹ nghệ cần cắt và gọt viên đá đó thành một viên đá cảnh có hình dạng là một khối trụ. Tính thể tích lớn nhất có thể của viên đá cảnh sau khi đã hoàn thiện.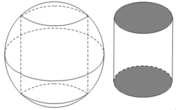
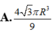
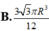
![]()
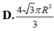
Một khối đá có hình là một khối cầu có bán kính R, người thợ thủ công mỹ nghệ cần cắt và gọt viên đá đó thành một viên đá cảnh có hình dạng là một khối trụ. Tính thể tích lớn nhất có thể của viên đá cảnh sau khi đã hoàn thiện
Đọc tiếp
Một khối đá có hình là một khối cầu có bán kính R, người thợ thủ công mỹ nghệ cần cắt và gọt viên đá đó thành một viên đá cảnh có hình dạng là một khối trụ. Tính thể tích lớn nhất có thể của viên đá cảnh sau khi đã hoàn thiện
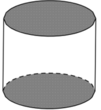
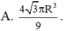
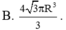
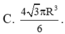
Một người thợ có một khối đá hình trụ có bán kính đáy bằng 30cm. Kẻ hai đường kính MN, PQ của hai đáy sao cho
M
N
⊥
P
Q
. Người thợ đó cắt khối đá theo các mặt cắt đi qua ba trong bốn điểm M, N, P,Q để được một khối đá có hình tứ diện (như hình vẽ dưới). Biết rằng khối tứ diện MNPQ có thể tích bằng
30
d
m
3
. Thể tích của lượng đá bị cắt bỏ gần với kết quả nào dưới đây nhất? A. ...
Đọc tiếp
Một người thợ có một khối đá hình trụ có bán kính đáy bằng 30cm. Kẻ hai đường kính MN, PQ của hai đáy sao cho M N ⊥ P Q . Người thợ đó cắt khối đá theo các mặt cắt đi qua ba trong bốn điểm M, N, P,Q để được một khối đá có hình tứ diện (như hình vẽ dưới). Biết rằng khối tứ diện MNPQ có thể tích bằng 30 d m 3 . Thể tích của lượng đá bị cắt bỏ gần với kết quả nào dưới đây nhất?
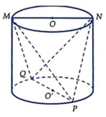
A. 111 , 4 d m 3
B. 111 , 39 d m 3
C. 111 , 30 d m 3
D. 111 , 35 d m 3
Một người thợ có một khối đá hình trụ. Kẻ hai đường kính MN, PQ của hai đáy sao cho MN
⊥
PQ. Người thợ đó cắt khối đá theo các mặt cắt đi qua 3 trong 4 điểm M, N, P, Q để thu được một khối đá có hình tứ diện MNPQ. Biết rằng MN 60 cm và thể tích của khối tứ diện MNPQ bằng 30
d
m
3
. Hãy tính thể tích của lượng đá bị cắt bỏ (làm tròn kết quả đến 1 chữ số thập ) A. 111,4
d
m
3
B. 121,3 ...
Đọc tiếp
Một người thợ có một khối đá hình trụ. Kẻ hai đường kính MN, PQ của hai đáy sao cho MN ⊥ PQ. Người thợ đó cắt khối đá theo các mặt cắt đi qua 3 trong 4 điểm M, N, P, Q để thu được một khối đá có hình tứ diện MNPQ. Biết rằng MN = 60 cm và thể tích của khối tứ diện MNPQ bằng 30 d m 3 . Hãy tính thể tích của lượng đá bị cắt bỏ (làm tròn kết quả đến 1 chữ số thập )
A. 111,4 d m 3
B. 121,3 d m 3
C. 101,3 d m 3
D. 141,3 d m 3
Một người thợ có một khối đá hình trụ. Kẻ hai đường kính MN, PQ của hai đáy sao cho MN
⊥
PQ. Người thợ đó cắt khối đá theo các mặt cắt đi qua 3 trong 4 điểm M, N, P, Q để thu được một khối đá có hình tứ diện MNPQ. Biết rằng MN 60 cm và thể tích của khối tứ diện MNPQ bằng
30
d
m
3
. Hãy tính thể tích của lượng đá bị cắt bỏ (làm tròn kết quả đến 1 chữ số thập phân)
Đọc tiếp
Một người thợ có một khối đá hình trụ. Kẻ hai đường kính MN, PQ của hai đáy sao cho MN ⊥ PQ. Người thợ đó cắt khối đá theo các mặt cắt đi qua 3 trong 4 điểm M, N, P, Q để thu được một khối đá có hình tứ diện MNPQ. Biết rằng MN = 60 cm và thể tích của khối tứ diện MNPQ bằng 30 d m 3 . Hãy tính thể tích của lượng đá bị cắt bỏ (làm tròn kết quả đến 1 chữ số thập phân)
![]()
![]()
![]()
![]()
Để tính diện tích xung quanh của một khối cầu bằng đá, người ta thả nó vào một chiếc thùng hình trụ có chiều cao 2m, bán kính đường tròn đáy 0,5m và có chứa sẵn một lượng nước có thể tích bằng
1
8
thể tích của thùng. Sau khi thả khối cầu bằng đá vào, người ta đo được mực nước trong thùng cao gấp 3 lần mực nước ban đầu khi chưa thả khối cầu bằng đá vào. Diện tích xung quanh của khối cầu bằng đá gần nhất với kết quả nào dưới đây ? A. ...
Đọc tiếp
Để tính diện tích xung quanh của một khối cầu bằng đá, người ta thả nó vào một chiếc thùng hình trụ có chiều cao 2m, bán kính đường tròn đáy 0,5m và có chứa sẵn một lượng nước có thể tích bằng 1 8 thể tích của thùng. Sau khi thả khối cầu bằng đá vào, người ta đo được mực nước trong thùng cao gấp 3 lần mực nước ban đầu khi chưa thả khối cầu bằng đá vào. Diện tích xung quanh của khối cầu bằng đá gần nhất với kết quả nào dưới đây ?
A. 2 , 6 m 2
B. 1 , 5 m 2
C. 3 , 4 m 2
D. 1 , 7 m 2
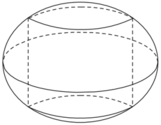
Có một khối cầu bằng gỗ bán kính R10cm. Sau khi cưa bằng hai chỏm cầu có bán kính đáy bằng một nửa R đối xứng nhau qua tâm khối cầu, một người thợ khoan xuyên tâm khối cầu. Người thợ đã khoan bỏ đi phần hình trụ có trục của nó trùng với trục hình cầu; mặt cắt của hình trụ vuông góc với trục hình trụ là một hình tròn có bán kính bằng 1/2R. Tính thể tích V của phần còn lại của khối cầu (làm tròn đến số thập phân thứ ba).
Đọc tiếp
Có một khối cầu bằng gỗ bán kính R=10cm. Sau khi cưa bằng hai chỏm cầu có bán kính đáy bằng một nửa R đối xứng nhau qua tâm khối cầu, một người thợ khoan xuyên tâm khối cầu. Người thợ đã khoan bỏ đi phần hình trụ có trục của nó trùng với trục hình cầu; mặt cắt của hình trụ vuông góc với trục hình trụ là một hình tròn có bán kính bằng 1/2R. Tính thể tích V của phần còn lại của khối cầu (làm tròn đến số thập phân thứ ba).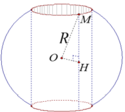
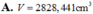
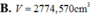
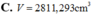
![]()
Một khúc gỗ có dạng hình khối nón có bán kính đáy bằng r2m, chiều cao h6m. Bác thợ mộc chế tác từ khúc gỗ đó thành một khúc gỗ có dạng hình khối trụ như hình vẽ. Gọi V là thể tích lớn nhất của khúc gỗ hình trụ sau khi chế tác. Tính V.
Đọc tiếp
Một khúc gỗ có dạng hình khối nón có bán kính đáy bằng r=2m, chiều cao h=6m. Bác thợ mộc chế tác từ khúc gỗ đó thành một khúc gỗ có dạng hình khối trụ như hình vẽ. Gọi V là thể tích lớn nhất của khúc gỗ hình trụ sau khi chế tác. Tính V.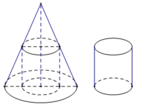
![]()
![]()
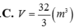
![]()
Một khúc gỗ có dạng hình khối nón có bán kính đáy bằng r2m, chiều cao h6m. Bác thợ mộc chế tác từ khúc gỗ đó thành một khúc gỗ có dạng hình khối trụ như hình vẽ. Gọi V là thể tích lớn nhất của khúc gỗ hình trụ sau khi chế tác. Tính V.
Đọc tiếp
Một khúc gỗ có dạng hình khối nón có bán kính đáy bằng r=2m, chiều cao h=6m. Bác thợ mộc chế tác từ khúc gỗ đó thành một khúc gỗ có dạng hình khối trụ như hình vẽ. Gọi V là thể tích lớn nhất của khúc gỗ hình trụ sau khi chế tác. Tính V.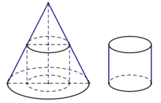
![]()
![]()
![]()
![]()
Một khối gỗ hình lập phương có thể tích
V
1
. Một người thợ mộc muốn gọt giũa khối gỗ đó thành một khối trụ có thể tích là
V
2
. Tính tỉ số lớn nhất
k
V
2
V
1
?
Đọc tiếp
Một khối gỗ hình lập phương có thể tích V 1 . Một người thợ mộc muốn gọt giũa khối gỗ đó thành một khối trụ có thể tích là V 2 . Tính tỉ số lớn nhất k = V 2 V 1 ?