Theo tính chất chất đường trung bình, ta chứng minh được tứ giác EFGH có 4 góc vuông và có 4cạnh bằng nhau.
Þ EFGH là hình vuông.
Đồng thời, G H = 1 2 A C = 3 c m . Suy ra SEFGH = GH2 = 9cm2
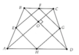
Theo tính chất chất đường trung bình, ta chứng minh được tứ giác EFGH có 4 góc vuông và có 4cạnh bằng nhau.
Þ EFGH là hình vuông.
Đồng thời, G H = 1 2 A C = 3 c m . Suy ra SEFGH = GH2 = 9cm2

Một hình thang cân có hai đường chéo vuông góc với nhau, độ dài đường chéo bằng 4cm. Tính diện tích tứ giác có đỉnh là trung điểm các cạnh của hình thang cân đó.
a) Cho hình thang cân có đường cao AH và các đường chéo vuông góc với nhau. Tính diện tích hình thang cân đó
b) Hai đường chéo của hình thang cân vuông góc với nhau, tổng hai cạnh đáy bằng 2a.Tính diện tích của hình thang theo a
GIÚP MÌNH VỚI MÌNH ĐANG CẦN GẤP
a tính diện tích hình thang cân có đường cao là h và các đường chéo vuông góc với nhau
b 2 đường chéo hình thang cân vuông góc với nhau tổng hai cạnh đáy =2a.Tính diện tính hình thang
1. chứng minh răng hình thang có hai đường chéo bằng nhay là hình thang cân.
2. cho hình thang ABCD (AB//CD), biết góc B- góc C= 240 và góc A= 1.5 góc D. Tính các góc của hình thang
3. Cho hình thang ABCD (AB//CD). các tia phân giác của góc A và góc B cắt nhau tại điểm E trên cạnh đáy CD. Chứng minh rằng CD=AD+BC.
4. Cho tam giác ABC vuông cân ở A. Trên nửa mặt phẳng bờ BC không chứa đỉnh A, vẽ BD vuông với BC và BD=BC.
a) tính các góc của hình thang
b) biết AB=5 cm. tính CD
5.Cho hình thang vuông ABCD có góc A= góc D = 900, đường chéo BD vuông góc với cạnh bên BC và BD=BC.
a) tính các góc của hình thang
b) biết AB=3cm. tính độ dài các cạnh BC,CD.
6. Hình thang cân ABCD có AB//CD, AB<CD. Kẻ hai đường cao AH, BK.
a) chứng minh ằng HD=KC.
7. Cho tam giác cân ABC (AB=AC), phân giác BD,CE.
a) tú giác BEDC là hình gì?Vì sao?
b)Chứng minh BE=ED=DC.
c) biết góc A=500. Tính các góc của tứ giác BEDC.
8. cho tam giác đều ABC, hai đường cao BN,CM
a) chứng minh tứ giác BMNC là hình thang cân
b) Tính chu vi của hình thang BMNC là hình thang cân
Cho hình thang cân ABCD (AB//CD) có đường chéo BD vuông góc với cạnh bên BC và đồng thời DB là tia phân giác của A D C ^ .
a) Tính các góc của hình thang cân ABCD.
b) Biết BC = 6 cm, tính chu vi và diện tích của hình thang cân ABCD
Một hình thang cân có đường cao =1/2 tổng 2 đáy. Tính góc tạo bởi 2 đường chéo của hình thang. Bài 4:nối 1 điểm O bên trì 1 hình thang cân với các đỉnh của nó. Cm từ 4 đoạn thẳng nhận đc có thể tạo thành 1 tứ giác nội tiếp hình thang đó( tứ giác có 4 đỉnh nằm trên cạnh hình thang). ( mình năm nay ms lên lớp 8 ms học trc đường Trung Bình thui
Cho hình thang cân ABCD có hai đường chéo vuông góc với nhau độ dài đường cao 3,(001) cm Tính diện tích của hình thag đó
Câu 31. Khẳng định đúng là
A. Hình thang cân là tứ giác có hai cạnh đối song song.
B. Trong hình thang cân hai đường chéo bằng nhau.
C. Hình thang cân là tứ giác có hai góc bằng nhau.
D. Hình thang cân là tứ giác có hai góc đối bằng nhau.
Có bạn nào biết công thức tính diện tích các đa giác đặc biệt hk ( Vd: hình thang cân có 2 đường chéo vuông góc, hình thang cân có một góc bằng 45 độ), giúp mình với....