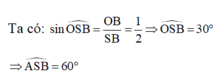Các câu hỏi tương tự
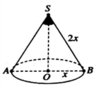
Cho hình nón có bán kính đáy bằng a, độ dài đường sinh bằng 2a. Góc ở đỉnh của hình nón bằng A.
30
o
B.
120
o
C.
60
o
D.
150
o
Đọc tiếp
Cho hình nón có bán kính đáy bằng a, độ dài đường sinh bằng 2a. Góc ở đỉnh của hình nón bằng
A. 30 o
B. 120 o
C. 60 o
D. 150 o
Cho hình nón (N) có đường cao SO h và bán kính đáy bằng R, gọi M là điểm trên đoạn SO, đặt OM x, 0 x h. (C ) là thiết diện của mặt phẳng (P) vuông góc với trục SO tại M, với hình nón (N). Tìm x để thể tích khối nón đỉnh O đáy là (C) lớn nhất A.
h
2
B.
h
2
2
C.
h
3...
Đọc tiếp
Cho hình nón (N) có đường cao SO = h và bán kính đáy bằng R, gọi M là điểm trên đoạn SO, đặt OM = x, 0 < x <h. (C ) là thiết diện của mặt phẳng (P) vuông góc với trục SO tại M, với hình nón (N). Tìm x để thể tích khối nón đỉnh O đáy là (C) lớn nhất
A. h 2
B. h 2 2
C. h 3 2
D. h 3
Cho hình chóp nón N có bán kính đáy bằng R, đường cao SO. Một mặt phẳng (P) cố định vuông góc với SO tại O’ và cắt khối nón theo hình nón có bán kính R’. Mặt phẳng (Q) thay đổi, vuông góc với SO tại điểm
O
1
(
O
1
nằm giữa O và O) cắt khối nón theo thiết diện là hình tròn có bán kính x.Tính xtheo R và R’ để (Q) chia phần khối nón nằm giữa (P) và đáy hình nón thành hai phần có thể tích...
Đọc tiếp
Cho hình chóp nón N có bán kính đáy bằng R, đường cao SO. Một mặt phẳng (P) cố định vuông góc với SO tại O’ và cắt khối nón theo hình nón có bán kính R’. Mặt phẳng (Q) thay đổi, vuông góc với SO tại điểm O 1 ( O 1 nằm giữa O và O') cắt khối nón theo thiết diện là hình tròn có bán kính x.Tính xtheo R và R’ để (Q) chia phần khối nón nằm giữa (P) và đáy hình nón thành hai phần có thể tích bằng nhau
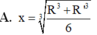
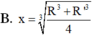
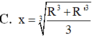
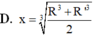
Cho biết hiệu đường sinh và bán kính đáy của một hình nón là a, góc giữa đường sinh và mặt đáy là
α
. Tính diện tích mặt cầu nội tiếp hình nón
Đọc tiếp
Cho biết hiệu đường sinh và bán kính đáy của một hình nón là a, góc giữa đường sinh và mặt đáy là α . Tính diện tích mặt cầu nội tiếp hình nón
![]()
![]()
![]()
![]()
Một hình nón có góc ở đỉnh bằng a, bán kính đường tròn đáy bằng a, diện tích xung quanh của hình nón bằng
Đọc tiếp
Một hình nón có góc ở đỉnh bằng a, bán kính đường tròn đáy bằng a, diện tích xung quanh của hình nón bằng
![]()
![]()
![]()
![]()
Một hình trụ có bán kính đáy bằng r và khoảng cách giữa hai đáy bằng
r
3
Một hình nón có đỉnh là tâm mặt đáy này và đáy trùng với mặt đáy kia của hình trụ. Tính tỉ số diện tích xung quanh của hình trụ và hình nón. D. 3
Đọc tiếp
Một hình trụ có bán kính đáy bằng r và khoảng cách giữa hai đáy bằng r 3 Một hình nón có đỉnh là tâm mặt đáy này và đáy trùng với mặt đáy kia của hình trụ. Tính tỉ số diện tích xung quanh của hình trụ và hình nón.
![]()
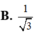
![]()
D. 3
Cho hình nón có diện tích xung quanh bằng
3
πa
2
và bán kính đáy bằng a. Độ dài đường sinh của hình nón đã cho bằng:
Đọc tiếp
Cho hình nón có diện tích xung quanh bằng 3 πa 2 và bán kính đáy bằng a. Độ dài đường sinh của hình nón đã cho bằng:
![]()
![]()
![]()
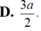
Một hình nón có bán kính đường tròn đáy bằng 3a và đường sinh bằng 5a. Thể tích khối nón là A.
9
πa
3
B.
12
πa
3
C.
5
πa
3
D.
15
πa
3
Đọc tiếp
Một hình nón có bán kính đường tròn đáy bằng 3a và đường sinh bằng 5a. Thể tích khối nón là
A. 9 πa 3
B. 12 πa 3
C. 5 πa 3
D. 15 πa 3
Cho hình cầu (S) tâm O, bán kính R. Hình cầu (S) ngoại tiếp một hình trụ tròn xoay (T) có đường cao bằng đường kính đáy và hình cầu (S) lại nội tiếp trong một hình nón tròn xoay (N) có góc ở đỉnh bằng
60
0
. Tính tỉ số thể tích của hình trụ (T) và hình nón (T) .
A
.
V
T
V
N
2...
Đọc tiếp
Cho hình cầu (S) tâm O, bán kính R. Hình cầu (S) ngoại tiếp một hình trụ tròn xoay (T) có đường cao bằng đường kính đáy và hình cầu (S) lại nội tiếp trong một hình nón tròn xoay (N) có góc ở đỉnh bằng 60 0 . Tính tỉ số thể tích của hình trụ (T) và hình nón (T) .
A . V T V N = 2 6
B . V T V N = 2 3
C . V T V N = 3 2
D. Đáp án khác