Gọi O là tâm đường tròn. Từ O kẻ bán kính vuông góc với BC, cắt BC ở G, cắt EF ở H.
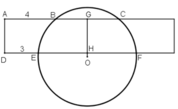
Ta có: G, H lần lượt là trung điểm BC và EF.
BG = BC/2 = 2,5
⇒ AG = AB + BG = 6,5
⇒ DH = AG = 6,5
⇒ EH = DH – DE = 3,5
⇒ EF = 2.EH = 7.
Vậy chọn đáp án B.
Gọi O là tâm đường tròn. Từ O kẻ bán kính vuông góc với BC, cắt BC ở G, cắt EF ở H.

Ta có: G, H lần lượt là trung điểm BC và EF.
BG = BC/2 = 2,5
⇒ AG = AB + BG = 6,5
⇒ DH = AG = 6,5
⇒ EH = DH – DE = 3,5
⇒ EF = 2.EH = 7.
Vậy chọn đáp án B.
Một hình chữ nhật cắt đường tròn như hình 121 biết AB = 4, BC = 5, DE = 3 (với cùng đơn vị đo).
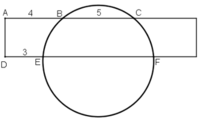
Độ dài EF bằng:
(A) 6; (B) 7; (C) 20/3; (D) 8
Cho đường tròn đường kính 10 cm, một đường thẳng d cách tâm O một khoảng bằng 3 cm.
1. Xác định vị trí tương đối của đường thẳng d và đường tròn (O).
2. Đường thẳng d cắt đường tròn (O) tại điểm A và B. Tính độ dài dây AB.
3. Kẻ đường kính AC của đường tròn (O). Tính độ dài BC và số đo góc CAB (làm tròn đến độ).
4. Tiếp tuyến của đường tròn (O) tại C cắt tia AB tại M. Tính độ dài BM.
Cho nửa đường tâm O , đường kính AB = 4 cm . Kẻ các tiếp tuyến Ax , By cùng phía với nửa đường tròn đối với AB . Gọi C là một điểm thuộc tia Ax . Kẻ tiếp tuyến CE với nửa đường tròn ( E là tiếp điểm ) , CE cắt By ở D .
a . Chứng minh rằng COOD = 90o ( Mình ko biết viết o ở trên không như trong sách ) .
b . Chứng minh rằng hình tam giác bằng chữ A ( ko biết viết hình ) AEB và hình tam giác bằng chữ A ( lại thế ) COD đồng dạng
c . Gọi I là trung điểm của CD . Vẽ đường tròn tâm I bán kính IC . Chứng minh rằng AB là tiếp tuyến của đường tròn ( i ) .
đ . Xác định vị trí của C trên tia Ax để có độ dài nhỏ nhất .
Bài 1:
a/ Cho hình vuông ABCD có cạnh 5cm. Chứng minh rằng: A, B, C, D cùng nằm trên một đường tròn, tính bán kính.
b/ Cho hình chữ nhật ABDE có AB = 8, BD = 6. Chứng minh rằng: A, B, D, E cùng nằm trên một đường tròn, tính bán kính.
Bài 2: Cho tam giác ABC, vẽ đường tròn tâm O đường kính BC. (O) cắt AB, AC lần lượt tại D và E, BE giao CD tại K.
a/ CMR: CD ^ AB, BE ^ AC.
b/ CMR: AK ^ BC.
Bài 3: Cho tam giác ABC vuông ở B, AB = 8cm, BC = 6cm. Gọi D là điểm đối xứng của điểm B qua AC.
a. CMR: 4 điểm A, B, C, D cùng thuộc một đường tròn. Tính bán kính của đường tròn đó.
b. Vẽ đường kính BE của đường tròn ngoại tiếp tam giác ABC. Chứng minh tứ giác ACDE là hinh thang cân.
Bài 1 : Cho hình vuông ABCD có cạnh bằng 3 cm . Chứng minh rằng : 4 đỉnh của hình vuông ABCD cùng nằm trên 1 đường tròn . Hãy tính bán kính đường tròn đó
Bài 2 : Cho tam giác nhọn ABC . Vẽ đường tròn tâm O , bán kính BC , nó cắt các cạnh AB, AC theo thứ tự ở D và E
a)CMR: CD vuông góc với AB , BE vuông góc với AC
b) gọi K là giao điểm của BE và CD. Chứng minh AK vuông góc BC
Bài 3:Cho hình thang ABCD , AB//CD, AB<CD , có góc C=góc D=60 độ , CD=2AD . Chứng minh 4 điểm A, B, C, D cùng thuộc 1 đường tròn. Tính diện tích đường tròn đó biết CD=4cm
Bài 4:Cho tam giác ABC vuông tại A. Trên AB, AC lần lượt lấy các điểm D, E . Gọi M, N, P, Q lần lượt là trung điểm của DE , EB, BC, CD. Chứng minh 4 điểm M, N, P, Q cùng thuộc 1 đường tròn
Cho hình chữ nhật ABCD biết AB=8;BC=15.Chứng minh rằng bốn điểm A,B,C,D, cùng thuộc 1 đường tròn và tính bán kính đường tròn đó
Cho tam giác ABC nhọn, hai đường cao BE và CF cắt nhau tại H
a, CM: tam giác BHC và tam giác FHE đồng dạng
b, Giả sử BH = 2; HE = 6 và CF = 7. Tính độ dài CH biết rằng CH>FH và đơn vị đo độ dài đoạn thẳng là cm
c, AH cắt BC tại D. Gọi M, K, N lần lượt là hình chiếu của D trên AB, CF và AC. CM: 3 điểm M, K, N thẳng hàng
1/ Cho đường tròn (O) đường kính AB và 1 điểm C trên đường tròn.Từ O kẻ 1 đường thảng song song với dây AC , đường thảng này cắt tiếp tuyến tại B của đường tròn ở điển C A) CM: OD là phân giác của góc BOC b) CN: CD là tiếp tuyến của đường tròn
2/ Cho đường tròn (O;R), H là điểm bên trong đường tròn (H không trùng với O). Vẽ đưởng kính AB đi qua H (HB < HA). Vẽ dây CD vuông góc với AB tại H. CMR:
a) Góc BCA = 90 độ b) CH . HD = HB . HA c) Biết OH = R/2. Tính diện tích tam giác ACD theo R
3/ Cho tam giác MAB, vẽ đường tròn (O) đường kính AB cắt MA ở C, cắt MB ở D. Kẻ AP vuông góc CD , BQ cuông góc CD. Gọi H là giao điểm AD và BC. CM:
a) CP = DQ b) PD . DQ = PA . BQ và QC . CP = PD . QD c) MH vuông góc AB\
4/ Cho đường tròn (O;5cm) đường kính AB, gọi E là 1 điểm trên AB sao cho BE = 2cm.Qua trung điểm kH của đoạn AE vẽ dây cung CD vuông góc AB.
a) Tứ giác ACED là hình gì? Vì sao? b)Gọi I là giao điểm của DE với BC. CMR:I thuộc đường tròn (O') đường kính EB
c) CM HI là tiếp điểm của đường tròn (O') d) Tính độ dài đoạn HI
5/ Cho đường tròn (0) đường kính AB = 2R. Gọi I là trung điểm của AO, qua I kẻ dây CD vuông góc với OA.
a) Tứ giác ACOD là hình gì? tại sao?
b) CM tam giác BCD đều
c) Tính chu vi và diện tích tam giác BCD theo R
6/ Cho tam giác ABC vuông tại A có đường cao AH. Biết AB = 9cm; BC = 15cm
a) Tính độ dài các cạnh AC, AH, BH, HC
b) Vẽ đường tròn tâm B, bán kính BA. Tia AH cắt (B) tại D. CM: CD là tiếp tuyến của (B;BA)
c) Vẽ đường kính DE. CM: EA // BC
d) Qua E vẽ tiếp tuyến d với (B). Tia CA cắt d tại F, EA cắt BF tại G. CM: CF = CD + EF và tứ giác AHBG là hình chữ nhật
7/ Cho đường tròn (O) đường kính AB, điểm M thuộc đường tròn. Vẽ điểm N đối xứng với A qua M. BN cắt đường tròn ở C. gọi E là giao điểm của AC và BM.
a) CMR: NE vuông góc AB
b) Gọi F là điểm đối xứng với E qua M. CMR: FA là tiếp tuyến của đường tròn (O)
c) CM: FN là tiếp tuyến của đường tròn (B;BA)
8/ Cho nửa đường tròn (O), đường kính AB.Từ một điểm M trên nửa đường tròn ta vẽ tiếp tuyến xy. Từ A ta vẽ AD vuông góc với xy tại D
a) CM: AD // OM
b) Kẻ BC vuông góc với xy tại C. CMR: MC = MD
Cho tam giác ABC vuông tại A Biết AB = 3 cm, BC = 5 cm
a, Giải tam giác vuông ABC (số đo góc làm tròn đến độ)
b, Từ B kẻ đường thẳng vuông góc với BC, đường thẳng này cắt đường thẳng AC tại D. Tính độ dài các đoạn thẳng AD, BD
c, Gọi E, F lần lượt là hình chiếu của A trên BC và BD. Chứng minh hai tam giác BEF và BDC đồng dạng