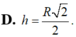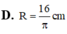Các câu hỏi tương tự
Người ta xếp 7 viên bi có cùng bán kính r vào một cái lọ hình trụ sao cho tất cả các viên bi đều tiếp xúc với đáy, viên bi nằm chính giữa tiếp xúc với 6 viên bi xung quanh và mỗi viên bi xung quanh đều tiếp xúc với các đường sinh của lọ hình trụ. Khi đó diện tích đáy của cái lọ hình trụ là
Đọc tiếp
Người ta xếp 7 viên bi có cùng bán kính r vào một cái lọ hình trụ sao cho tất cả các viên bi đều tiếp xúc với đáy, viên bi nằm chính giữa tiếp xúc với 6 viên bi xung quanh và mỗi viên bi xung quanh đều tiếp xúc với các đường sinh của lọ hình trụ. Khi đó diện tích đáy của cái lọ hình trụ là
![]()
![]()
![]()
![]()
Một bồn nước inox được thiết kế có dạng hình trụ (có nắp) đựng được
10
m
3
nước. Tìm bán kính R của đáy bồn nước, biết lượng inox được sử dụng để làm bồn nước là ít nhất (bỏ qua độ dày của bồn) A.
R
5
2
π
3
m
B.
R...
Đọc tiếp
Một bồn nước inox được thiết kế có dạng hình trụ (có nắp) đựng được 10 m 3 nước. Tìm bán kính R của đáy bồn nước, biết lượng inox được sử dụng để làm bồn nước là ít nhất (bỏ qua độ dày của bồn)
A. R = 5 2 π 3 m
B. R = 5 π 3 m
C. R = 10 π 3 m
D. R = 5 π 3 m
Một viên phấn bảng có dạng một khối trụ với bán kính đáy bằng 0,5cm, chiều dài 6cm. Người ta làm một hình hộp chữ nhật bằng carton đựng các viên phấn đó với kích thước 6cm x 5cm x 6cm. Hỏi cần ít nhất bao nhiêu hộp kích thước như trên để xếp 460 viên phấn? A. 17 B. 15 C. 16 D. 18
Đọc tiếp
Một viên phấn bảng có dạng một khối trụ với bán kính đáy bằng 0,5cm, chiều dài 6cm. Người ta làm một hình hộp chữ nhật bằng carton đựng các viên phấn đó với kích thước 6cm x 5cm x 6cm. Hỏi cần ít nhất bao nhiêu hộp kích thước như trên để xếp 460 viên phấn?
A. 17
B. 15
C. 16
D. 18
Một người cần làm một hình lăng trụ tam giác đều từ tấm nhựa phẳng để có thể tích là
6
3
c
m
3
. Để ít hao tốn vật liệu nhất thì cần tính độ dài các cạnh của khối lăng trụ tam giác đều này bằng bao nhiêu? A. Cạnh đáy bằng 4
3
và cạnh bên bằng
1
2
cm B. Cạnh đáy bằng
2
6
v...
Đọc tiếp
Một người cần làm một hình lăng trụ tam giác đều từ tấm nhựa phẳng để có thể tích là 6 3 c m 3 . Để ít hao tốn vật liệu nhất thì cần tính độ dài các cạnh của khối lăng trụ tam giác đều này bằng bao nhiêu?
A. Cạnh đáy bằng 4 3 và cạnh bên bằng 1 2 cm
B. Cạnh đáy bằng 2 6 và cạnh bên bằng 1 cm
C. Cạnh đáy bằng 2 2 và cạnh bên bằng 3 cm
D. Cạnh đáy bằng 2 3 và cạnh bên bằng 2cm
Người ta làm chiếc thùng phi dạng hình trụ, kín hai đáy, với thể tích theo yêu cầu là
2
πm
3
. Hỏi bán kính đáy R và chiều cao h của thùng phi bằng bao nhiêu để khi làm thì tiết kiệm vật liệu nhất? A.
R
2
m
,
h
1
2
B.
R
...
Đọc tiếp
Người ta làm chiếc thùng phi dạng hình trụ, kín hai đáy, với thể tích theo yêu cầu là 2 πm 3 . Hỏi bán kính đáy R và chiều cao h của thùng phi bằng bao nhiêu để khi làm thì tiết kiệm vật liệu nhất?
A. R = 2 m , h = 1 2
B. R = 4 m , h = 1 8
C. R = 1 2 m , h = 8 m
D. R = 1 m , h = 2 m
Một xưởng sản xuất những thùng bằng kẽm hình hộp chữ nhật không có nắp và có các kích thước x, y, z (dm). Biết tỉ số hai cạnh đáy là x : y 1 : 3 thể tích của khối hộp bằng 18 lít. Để tốn ít vật liệu nhất thì bộ số x, y, z là A. x 2, y 6, z
3
2
B. x 1, y 3, z 6 C. x
3
2
,
y
9
2
,...
Đọc tiếp
Một xưởng sản xuất những thùng bằng kẽm hình hộp chữ nhật không có nắp và có các kích thước x, y, z (dm). Biết tỉ số hai cạnh đáy là x : y = 1 : 3 thể tích của khối hộp bằng 18 lít. Để tốn ít vật liệu nhất thì bộ số x, y, z là
A. x= 2, y = 6, z = 3 2
B. x =1, y = 3, z =6
C. x= 3 2 , y = 9 2 , z = 3 2
D.x= 1 2 , y= 3 2 , z= 24
Khi cắt mặt cầu S (O; R) bởi một mặt kính đi qua tâm O, ta được hai nửa mặt cầu giống nhau. Giao tuyến của mặt kính đó với mặt cầu gọi là mặt đáy của mỗi nửa mặt cầu. Một hình trụ gọi là nội tiếp nửa mặt cầu S (O; R) nếu một đáy của hình trụ nằm trong đáy của nửa mặt cầu, còn đường tròn đáy kia là giao tuyến của hình trụ với nửa mặt cầu. Biết R 1, tính bán kính đáy r và chiều cao h của hình trụ nội tiếp nửa mặt cầu S(O; R) để khối trụ có thể tích lớn nhất.
Đọc tiếp
Khi cắt mặt cầu S (O; R) bởi một mặt kính đi qua tâm O, ta được hai nửa mặt cầu giống nhau. Giao tuyến của mặt kính đó với mặt cầu gọi là mặt đáy của mỗi nửa mặt cầu. Một hình trụ gọi là nội tiếp nửa mặt cầu S (O; R) nếu một đáy của hình trụ nằm trong đáy của nửa mặt cầu, còn đường tròn đáy kia là giao tuyến của hình trụ với nửa mặt cầu. Biết R = 1, tính bán kính đáy r và chiều cao h của hình trụ nội tiếp nửa mặt cầu S(O; R) để khối trụ có thể tích lớn nhất.
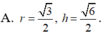


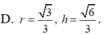
Một hình trụ có bán kính đáy bằng r và khoảng cách giữa hai đáy bằng
r
3
Một hình nón có đỉnh là tâm mặt đáy này và đáy trùng với mặt đáy kia của hình trụ. Tính tỉ số diện tích xung quanh của hình trụ và hình nón. D. 3
Đọc tiếp
Một hình trụ có bán kính đáy bằng r và khoảng cách giữa hai đáy bằng r 3 Một hình nón có đỉnh là tâm mặt đáy này và đáy trùng với mặt đáy kia của hình trụ. Tính tỉ số diện tích xung quanh của hình trụ và hình nón.
![]()
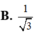
![]()
D. 3
Cho mặt cầu (S) có bán kính R. Một hình trụ có chiều cao h và bán kính đáy r thay đổi nội tiếp mặt cầu. Tính chiều cao h theo R sao cho diện tích xung quanh của hình trụ lớn nhất.
Đọc tiếp
Cho mặt cầu (S) có bán kính R. Một hình trụ có chiều cao h và bán kính đáy r thay đổi nội tiếp mặt cầu. Tính chiều cao h theo R sao cho diện tích xung quanh của hình trụ lớn nhất.
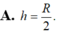
![]()
![]()