Từ công thức l = Rα (α có đơn vị là rad) ta có:
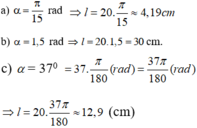
Từ công thức l = Rα (α có đơn vị là rad) ta có:
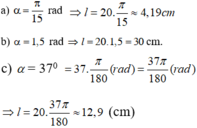
Một đường tròn có bán kính 25 cm. Tìm độ dài của các cung trên đường tròn có số đo 49 ο
Một đường tròn có bán kính 25 cm. Tìm độ dài của các cung trên đường tròn có số đo 3π / 7
Một đường tròn có bán kính 25 cm. Tìm độ dài của các cung trên đường tròn có số đo 4 / 3
Một đường tròn có bán kính R = 10 π .Tìm độ dài của cung có số đo π/2 trên đường tròn.
A. 10cm.
B. 5cm.
C. 20 π 2 c m
D. π 2 20 cm.
Một đường tròn có bán kính R = 5(cm). Độ dài của cung trên đường tròn có số đo 135 ° là:
A. 3 π 4
B. 5 π 4
C. 15 π 4
D. 15 π 2
Một đường tròn có bán kính 20 cm. Hỏi độ dài của cung trên đường tròn đó có số đo π/15 gần với giá trị nào nhất.
A. 4,1
B. 4,2
C. 4,3
D. 4,4
Trên đường tròn lượng giác bán kính 15cm, độ dài cung có số đo 3,4 rad là:
A. 51cm
B. 102cm
C. 160,14cm
D. 160,22cm
Cho đường tròn có bán kính 6cm . Tìm số đo (rad) của cung có độ dài là 3cm :
A. 0,5
B. 3
C. 2
D. 1
Độ dài của cung có số đo π/2 rad, trên đường tròn bán kính r=20 là:
A. l = π 40
B. l = 40 π
C. l = 5 π
D. l = 10 π