Các câu hỏi tương tự
cho hình vuông ABCD có cạnh bằng 12 cm các điểm E, F ,G theo thứ tự thuộc AD,AB,CE sao cho AE//FG//BC và EF//BG gọi S tam giác AEF,EFG, FGB,GBC theo thứ tự là S1,S2,S3,S4bieets S1:S2:S3:S4=1:2:4:8
a) tính FG,AF,FB,AE
b)tính diện tích của S1,S2,S3,S4
cho s1=81; s2=s1+225; s3=s1+s2+625;s4=s1+s2+s3+1521;s5=s1+s2+s3+s4+3249
tính s25;s50;s100
Mn giúp mik bt Tin Học với ạ..! Mn lm đc bài nào thì làm nha ...!Câu 1 (7,0 điểm): Số chính phương.Cho trước số nguyên dương N (0 N≤ 106 ). Yêu cầu: Tìm số nguyên dương K nhỏ nhất sao cho tích của K và N là một số chính phương. Dữ liệu vào: File CP.INP chứa số N. Dữ liệu ra: File CP.OUT ghi số nguyên K tìm được.Câu 2 (6,0 điểm): Dòng lớn nhất.Cho một tệp tin gồm nhiều dòng. Trên mỗi dòng chứa một xâu kí tự chỉ gồm các kí tự chữ cái và chữ số, độ dài của mỗi xâu không quá 255 kí tự.Yêu cầu: Đưa r...
Đọc tiếp
Mn giúp mik bt Tin Học với ạ..! Mn lm đc bài nào thì làm nha ...!
Câu 1 (7,0 điểm): Số chính phương.
Cho trước số nguyên dương N (0< N≤ 106 ). Yêu cầu: Tìm số nguyên dương K nhỏ nhất sao cho tích của K và N là một số chính phương. Dữ liệu vào: File CP.INP chứa số N. Dữ liệu ra: File CP.OUT ghi số nguyên K tìm được.
Câu 2 (6,0 điểm): Dòng lớn nhất.
Cho một tệp tin gồm nhiều dòng. Trên mỗi dòng chứa một xâu kí tự chỉ gồm các kí tự chữ cái và chữ số, độ dài của mỗi xâu không quá 255 kí tự.
Yêu cầu: Đưa ra dòng có nhiều kí tự chữ cái nhất, nếu có nhiều dòng thỏa mãn thì đưa ra dòng đầu tiên có nhiều kí tự chữ cái nhất. Dữ liệu vào: File DLN.INP gồm:
+ Dòng đầu ghi số N là số lượng dòng chứa các xâu kí tự.
+ N dòng tiếp theo: mỗi dòng ghi một xâu kí tự. Dữ liệu ra: File DLN.OUT ghi ra dòng có nhiều kí tự chữ cái nhất, nếu có nhiều dòng thỏa mãn thì đưa ra dòng đầu tiên có nhiều kí tự chữ cái nhất.
Câu 3 (4,0 điểm): Dãy con đối xứng.
Một dãy số liên tiếp gọi là dãy đối xứng nếu đọc các số theo thứ tự từ trái sang phải cũng giống như khi đọc theo thứ tự từ phải sang trái. Cho dãy số A gồm N số nguyên dương: a1, a2,..., aN (1≤ N≤ 10000; 1≤ ai≤ 32000; 1≤ i≤ N)
Yêu cầu: Hãy tìm dãy con đối xứng dài nhất của dãy A. Nếu có nhiều dãy con thoả mãn thì lấy dãy con xuất hiện đầu tiên trong dãy A. Dữ liệu vào: File DX.INP gồm 2 dòng:
- Dòng 1: ghi số nguyên dương N.
- Dòng 2: ghi N số nguyên dương lần lượt là giá trị của các số trong dãy A, các số được ghi cách nhau ít nhất một dấu cách.
Dữ liệu ra: File DX.OUT ghi dãy tìm được trên cùng một dòng, các số được ghi cách nhau một dấu cách.
Câu 4 (3,0 điểm): Dãy nguyên tố.
Cho một dãy số B gồm n số nguyên dương (n ≤ 1000), mỗi phần tử trong dãy có giá trị không quá 30000. Yêu cầu:
+ Tìm dãy con dài nhất (liên tiếp hoặc không liên tiếp) các phần tử là những số nguyên tố có giá trị tăng dần của dãy B và thứ tự của các phần tử không đổi so với ban đầu. Ví dụ: Dãy 8 phần tử {4, 2, 5, 6, 3, 3, 7, 9} có dãy con nguyên tố tăng dài nhất là {2, 5, 7}.
+ Nếu có nhiều dãy con thoả mãn thì lấy dãy con xuất hiện đầu tiên trong dãy B. Dữ liệu vào: File NT.INP gồm 2 dòng:
- Dòng 1: Ghi số nguyên dương n.
- Dòng 2: Ghi n số nguyên dương, các số được ghi cách nhau một dấu cách. Dữ liệu ra: File NT.OUT ghi dãy con tìm được trên cùng 1 dòng, giữa 2 phần tử liền kề trong dãy có một dấu cách.
Cho hình bs.32 (tam giác MNP vuông tại đỉnh M và NRQP, PUTM, MKHN đều là hình vuông, còn
S
1
,
S
2
,
S
3
tương ứng là diện tích của một hình). Quan hệ nào sau đây là đúng?(A)
S
3...
Đọc tiếp
Cho hình bs.32 (tam giác MNP vuông tại đỉnh M và NRQP, PUTM, MKHN đều là hình vuông, còn S 1 , S 2 , S 3 tương ứng là diện tích của một hình). Quan hệ nào sau đây là đúng?
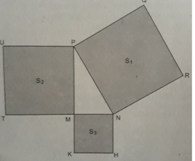
(A) S 3 + S 2 = S 1
(B) S 3 2 + S 2 2 = S 1 2
(C) S 3 + S 2 > S 1
(D) S 3 2 + S 2 2 < S 1 2
1.Viết chương trình tìm giá trị lớn nhất của một mảng chứa các số Z gồm N phần tử.
2.Viết chương trình nhập vào một mảng gồm N số nguyên. Sắp xếp lại mảng theo thứ tự tăng dần và in ra kết quả màn hình.
3.Viết chương trình nhập vào một mảng A gồm N số nguyên và nhập thêm vào một số nguyên X. Hãy kiểm tra xem phần tử X có trong mảng A hay không ?
1/Cho một dãy số N phần tử . Viết chương trình sắp xếp các phần tử đã cho theo thứ tự tăng dần (giảm dần)
2/ Viết chương trình chèn thêm 1 số nguyên vào 1 dãy số nguyên đã được sắp xếp theo thứ tự tăng dần sao cho dãy số không thay đổi trật tự sắp xếp
GIÚP MIK VỚI SẮP KT 1 TIẾT RÙI!!!!!!!!!!!!!........
Cho hình thang ABCD,đáy lớn là CD.Gọi O la giao điểm của AC và BD.Các đường kể từ A và B song song với BC VÀ AD cắt các đường chéoBD và AC ,tương ứng ở F và E.Chứng minh EF//AB
b. AB2=EF.CD.
c. gọi S1,S2,S3,S4 theo thứ tự là diện tích của các tam giác OAB,OCD,OAD ,OBC
Chứng minh S1.S2=S3.S4
Cho hình thang ABCD (đáy lớn CD), gọi O là giao điểm của AC và BD; các đường kẻ từ A và B lần lượt song song với BC và AD cắt các đường chéo BD và AC tương ứng ở F và E. Chứng minh:
a) EF // AB
b) 2AB = EF . CD
c) Gọi S1 ;S2 ;S3 ;S4 theo thứ tự là diện tích của các tam giác OAB; OCD; OAD và OBC
Chứng minh: S1 . S2 = S3 . S4
Cho hình thang ABCD (đáy lớn CD), gọi O là giao điểm của AC và BD; các đường kẻ từ A và B lần lượt song song với BC và AD cắt các đường chéo BD và AC tương ứng ở F và E. Chứng minh:
a) EF // AB
b) 2AB = EF . CD
c) Gọi S1 ;S2 ;S3 ;S4 theo thứ tự là diện tích của các tam giác OAB; OCD; OAD và OBC
Chứng minh: S1 . S2 = S3 . S4










