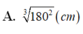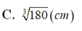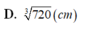Các câu hỏi tương tự
Khi sản xuất vỏ lon sữa bò hình trụ, các nhà thiết kế đặt mục tiêu sao cho chi phí nguyên liệu làm vỏ hộp ít nhất (diện tích toàn phần của lon nhỏ nhất). Bán kính đáy của vỏ lon là bao nhiêu khi muốn thể tích của lon là 314
c
m
3
. A.
r
314
4
π...
Đọc tiếp
Khi sản xuất vỏ lon sữa bò hình trụ, các nhà thiết kế đặt mục tiêu sao cho chi phí nguyên liệu làm vỏ hộp ít nhất (diện tích toàn phần của lon nhỏ nhất). Bán kính đáy của vỏ lon là bao nhiêu khi muốn thể tích của lon là 314 c m 3 .
A. r = 314 4 π 3 c m
B. r = 942 2 π 3 c m
C. r = 314 2 π 3 c m
D. r = 314 π 3 c m
Cần sản xuất một vỏ hộp sữa hình trụ có thể tích V cho trước. Để tiết kiệm vật liệu nhất thì bán kính đáy phải bằng
Đọc tiếp
Cần sản xuất một vỏ hộp sữa hình trụ có thể tích V cho trước. Để tiết kiệm vật liệu nhất thì bán kính đáy phải bằng
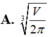
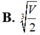
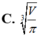
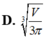
Khi sản xuất vỏ lon sữa bò hình trụ có thể tích là V, các nhà thiết kế luôn đặt mục tiêu sao cho chi phí nguyên liệu làm vỏ lon sữa bò là ít nhất, tức là diện tích toàn phần của hình trụ là nhỏ nhất. Muốn thể tích khối trụ bằng V và diện tích toàn phần hình trụ nhỏ nhất thì bán kính đáy bằng bao nhiêu? A.
r
V
π
2...
Đọc tiếp
Khi sản xuất vỏ lon sữa bò hình trụ có thể tích là V, các nhà thiết kế luôn đặt mục tiêu sao cho chi phí nguyên liệu làm vỏ lon sữa bò là ít nhất, tức là diện tích toàn phần của hình trụ là nhỏ nhất. Muốn thể tích khối trụ bằng V và diện tích toàn phần hình trụ nhỏ nhất thì bán kính đáy bằng bao nhiêu?
A. r = V π 2 3
B. r = V 3
C. r = V 2 π 3
D. r = V 2 3
Từ một nguyên vật liệu cho trước, một công ty muốn thiết kế bao bì để đựng sữa với thể tích 1dm3. Bao bì được thiết kế bởi một trong hai mô hình sau: hình hộp chữ nhật có đáy là hình vuông; hoặc hình trụ. Hỏi thiết kế theo mô hình nào sẽ tiết kiệm được nguyên vật liệu nhất? Và thiết kế mô hình đó theo kích thước như thế nào?
Đọc tiếp
Từ một nguyên vật liệu cho trước, một công ty muốn thiết kế bao bì để đựng sữa với thể tích 1dm3. Bao bì được thiết kế bởi một trong hai mô hình sau: hình hộp chữ nhật có đáy là hình vuông; hoặc hình trụ. Hỏi thiết kế theo mô hình nào sẽ tiết kiệm được nguyên vật liệu nhất? Và thiết kế mô hình đó theo kích thước như thế nào?

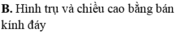

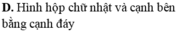
Khi sản xuất hộp mì tôm các nhà sản xuất luôn để một khoảng trống dưới đáy hộp. Hình vẽ dưới mô tả cấu trúc của hộp mì tôm. Thớ mì tôm có dạng hình trụ, hộp mì có dạng hình nón cụt được cắt ra bởi hình nón có chiều cao và bán kính đáy . Nhà sản xuất tìm cách sao cho thớ mì tôm có được thể tích lớn nhất vì mục đích thu hút khách hàng. Tìm thể tích lớn nhất đó. A.
48
π
B.
81...
Đọc tiếp
Khi sản xuất hộp mì tôm các nhà sản xuất luôn để một khoảng trống dưới đáy hộp. Hình vẽ dưới mô tả cấu trúc của hộp mì tôm. Thớ mì tôm có dạng hình trụ, hộp mì có dạng hình nón cụt được cắt ra bởi hình nón có chiều cao và bán kính đáy . Nhà sản xuất tìm cách sao cho thớ mì tôm có được thể tích lớn nhất vì mục đích thu hút khách hàng. Tìm thể tích lớn nhất đó.
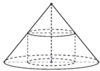
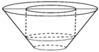
A. 48 π
B. 81 2 π
C. 36 π
D. 54 π
Từ một nguyên liệu cho trước, một công ti muốn thiết kế bao bì đựng sữa với thể tích 100ml3. Bao bì được thiết kế bởi một trong hai mô hình là: hình hộp chữ nhật có đáy là hình vuông và hình trụ. Hỏi thiết kế theo mô hình nào tiết kiệm nguyên vật liệu nhất ?
Đọc tiếp
Từ một nguyên liệu cho trước, một công ti muốn thiết kế bao bì đựng sữa với thể tích 100ml3. Bao bì được thiết kế bởi một trong hai mô hình là: hình hộp chữ nhật có đáy là hình vuông và hình trụ. Hỏi thiết kế theo mô hình nào tiết kiệm nguyên vật liệu nhất ?

Một xưởng sản xuất những thùng bằng kẽm hình hộp chữ nhật không có nắp và có các kích thước x, y, z (dm). Biết tỉ số hai cạnh đáy là x:y1:3 và thể tích của hộp bằng 18
d
m
3
Để tốn ít vật liệu nhất thì tổng x+y+z bằng? A.
26
3
B. 10. C.
19
2
D. 26.
Đọc tiếp
Một xưởng sản xuất những thùng bằng kẽm hình hộp chữ nhật không có nắp và có các kích thước x, y, z (dm). Biết tỉ số hai cạnh đáy là x:y=1:3 và thể tích của hộp bằng 18 d m 3 Để tốn ít vật liệu nhất thì tổng x+y+z bằng?
A. 26 3
B. 10.
C. 19 2
D. 26.
Cho hai tấm tôn hình chữ nhật đều có kích thước 1,5mx8m. Tấm tôn thứ nhất được chế tạo thành một hình hộp chữ nhật không đáy, không nắp, có thiết diện ngang là một hình vuông (mặt phẳng vuông góc với đường cao của hình hộp và cắt các mặt bên của hình hộp theo các đoạn giao tuyến tạo thành một hình vuông) và có chiều cao 1,5m, còn tấm tôn thứ hai được chế tạo thành một hình trụ không đáy, không nắp và cũng có chiều cao 1,5m. Gọi
V
1
,
V...
Đọc tiếp
Cho hai tấm tôn hình chữ nhật đều có kích thước 1,5mx8m. Tấm tôn thứ nhất được chế tạo thành một hình hộp chữ nhật không đáy, không nắp, có thiết diện ngang là một hình vuông (mặt phẳng vuông góc với đường cao của hình hộp và cắt các mặt bên của hình hộp theo các đoạn giao tuyến tạo thành một hình vuông) và có chiều cao 1,5m, còn tấm tôn thứ hai được chế tạo thành một hình trụ không đáy, không nắp và cũng có chiều cao 1,5m. Gọi
V
1
,
V
2
, theo thứ tự là thể tích của khối hộp chữ nhật và thể tích của khối trụ. Tính tỉ số
V
1
V
2
.

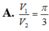
![]()
![]()
![]()
Một công ty Container cần thiết kết các thùng đựng hàng hình hộp chữ nhật, không nắp, có đáy hình vuông, thể tích là
108
m
3
. Tìm tổng diện tích nhỏ nhất của các mặt xung quanh và mặt đáy
Đọc tiếp
Một công ty Container cần thiết kết các thùng đựng hàng hình hộp chữ nhật, không nắp, có đáy hình vuông, thể tích là 108 m 3 . Tìm tổng diện tích nhỏ nhất của các mặt xung quanh và mặt đáy
![]()
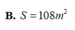
![]()
![]()