Ta có BC < BD mà C, D nằm cùng phía so với B ⇒ C nằm giữa B và D.

Ta có BC < BD mà C, D nằm cùng phía so với B ⇒ C nằm giữa B và D.

Một cách chứng minh khác của định lí 2:
Cho hình 13. Dùng quan hệ giữa góc và cạnh đối diện trong một tam giác để chứng minh rằng:
Nếu BC < BD thì AC < AD
Trong tam giác ACD, cạnh nào lớn nhất, tại sao?
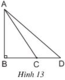
Cho tam giác ABD vuông tại B có C nằm Giữa B và D. Dùng quan hệ giữa góc và cạnh đối diện trong một tam giác để chứng minh: Nếu BC<BD thì AC<AD
1.Cho tam giác ABC có Â=90. Trên tia đối của tia AC lấy điểm D soa cho AD<AC. Nối B với D. Chứng minh: BC>BD(Chỉ sử dụng quan hệ giữa góc và cạnh đối diện)
2. Cho tam giác ABC. Chứng minh rằng AB+AC>BC(sử dụng qh giữa góc và cạnh đối diện)
3.Cho tam giác ABC(AB=AC), D là điểm bất kì trong tam giác sao cho ADB>ADC. Chứng minh rằng DC>DB(sd qh giữa góc và cạnh đối diện)
mik cần gấp, ai đúng và nhanh mik sẽ tick!!!
cho tam giác abc nhọn có AB<AC . Tia phân giác góc A cắt BC tại D . Chứng minh rằng DB<DC ( bài này là quan hệ giữa góc và cạnh đối diện trong 1 tam giác nha)
Cho tam giác ABC. Trên tia đối của AB lấy điểm D sao cho AC = AD
Khi đó AB + AC = AB + AD = BD, còn ACD là tam giác cân, nên góc ACD = góc ADC, tức là góc BDC = góc ACD
Mặt khác, do tia CA nằm giữa CB và CD nên góc BCD > góc DCA
Khi đó, trong tam giác BCD có: góc BCD > góc BDC nên BD > BC hay AB + AC > BC
Tương tự, em hãy chứng minh, trong tam giác ABC có: CA + CB > AB và BA + BC > CA
Câu 1: Cho tam giác ABC cân tại A. Trên cạnh BC lấy điểm D(D khác B,C). Trên tia đối của tia CB, lấy điểm E sao cho CE=BD. Đường vuông góc với BC kẻ từ E cắt tia AC tại N. MN cắt BC tại I.
1) Chứng minh rằng: DM=EN
2) Chứng minh rằng: IM=IN;BC<MN
3) Gọi O là giao của đường phân giác góc A và đường thẳng vuông góc với MN tại I.
Chứng minh rằng: Tam giác BMO= Tam giác CNO. Từ đó suy ra điểm O cố định.
Câu 2: Cho tam giác ABC cân tại A. Trên đường trung tuyến BD lấy điểm E sao cho góc DAE góc ABD (E nằm giữa B và D). Chứng minh rằng: Góc DAE= Góc ECB
Câu 1: Cho tam giác ABC cân tại A. Trên cạnh BC lấy điểm D(D khác B,C). Trên tia đối của tia CB, lấy điểm E sao cho CE=BD. Đường vuông góc với BC kẻ từ E cắt tia AC tại N. MN cắt BC tại I.
1) Chứng minh rằng: DM=EN
2) Chứng minh rằng: IM=IN;BC<MN
3) Gọi O là giao của đường phân giác góc A và đường thẳng vuông góc với MN tại I.
Chứng minh rằng: Tam giác BMO= Tam giác CNO. Từ đó suy ra điểm O cố định.
Câu 2: Cho tam giác ABC cân tại A. Trên đường trung tuyến BD lấy điểm E sao cho góc DAE góc ABD (E nằm giữa B và D). Chứng minh rằng: Góc DAE= Góc ECB
Cho tam giác ABC, AB < AC và AD là tia phân giác của góc A (D\(\in\)BC) .Kẻ AH\(⊥\)BC. M là trung điểm của cạnh BC.CMR: Tia AD nằm giữa AH và AM. giải chi tiết cho mình nha,mình mới tích(gợi ý: dùng quan hệ giữa góc và cạnh đối diện trong tam giác, định lí là:tam giác ABC có AB=DE,góc A < góc D,AC=DF thì BC<EF hoặc ngược lại)
Cho tam giác ABC có AB < AC, tia phân giác của góc A cắt cạnh BC tại I. Trên cạnh AC lấy điểm D sao cho AD = AB
a) Chứng minh rằng BI = ID
b) Tia DI cắt tia AB tại E. Chứng minh rằng ∆IBE = ∆IDC
c) Chứng minh BD // EC
d) Cho góc ABC = góc ACD. Chứng minh AB + BI = AC