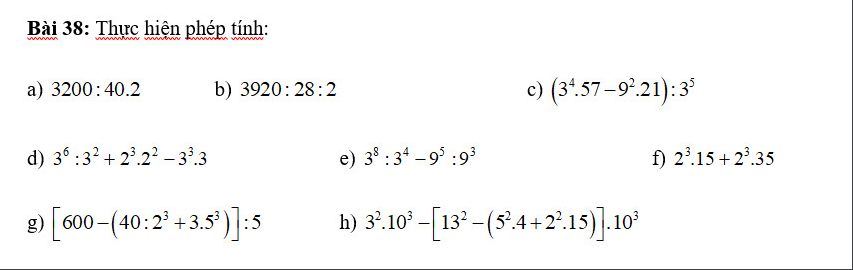\(Bài38\)
\(a.3200:40\cdot2=80\cdot2=160.\)
\(b.3920:28:2=140:2=70.\)
\(c.\left(3^4\cdot57-9^2\cdot21\right):3^5=\left(81\cdot57-81\cdot21\right):243=2916:243=12.\)
\(d.3^6:3^2+2^3\cdot2^2-3^3\cdot3=3^4+2^5-3^4=3^4-3^4+2^5=2^5=32.\)
\(e.3^8:3^4-9^5:9^3=\left(3^8:3^4\right)-\left(9^5:9^3\right)=3^4:9^2=81-81=0.\)
\(f.2^3\cdot15+2^3\cdot35=8\cdot15+8\cdot35=120+280=400.\)
\(g.\left[600-\left(40:2^3+3\cdot5^3\right)\right]:5=\left[600-\left(40\cdot8+3\cdot125\right)\right]:5\)
\(=\left[600-695\right]:5=-95:5=-19.\)
\(h.3^2\cdot10^3-\left[13^2-\left(5^2\cdot4+2^2\cdot15\right)\right]\cdot10^3\)
\(=9\cdot1000-\left[169-\left(25\cdot4+4\cdot15\right)\right]\cdot1000\)
\(=9000-\left[169-160\right]\cdot1000=9000-9\cdot1000\)
\(=9000-9000=0.\)