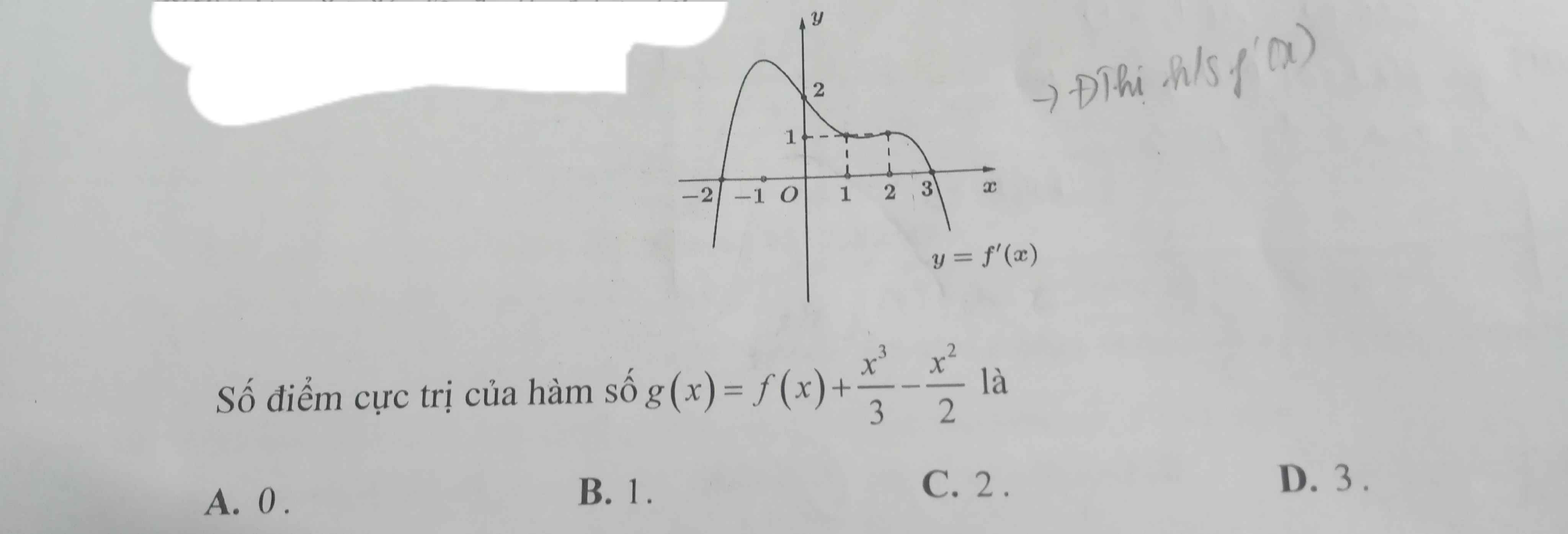Người ta đề có lẽ hơi nhầm lẫn 1 xíu, chỉ dựa trên đồ thị này thì ko có căn cứ nào để kết luận hàm đã cho có bao nhiêu cực trị cả
\(g'\left(x\right)=f'\left(x\right)+x^2-x=0\Leftrightarrow f'\left(x\right)=-x^2+x\)
Dễ dàng phác thảo đồ thị \(y=-x^2+x\) lên cùng hệ trục thì ta thấy 2 nhánh của \(y=-x^2+x\) (cũng quay xuống dưới) có thể cắt 2 nhánh của \(f'\left(x\right)\) tại 0, 1 hay 2 điểm đều được (vì ko ai biết bên dưới 2 nhánh của \(f'\left(x\right)\) kia sẽ diễn tiếp tiếp thế nào)