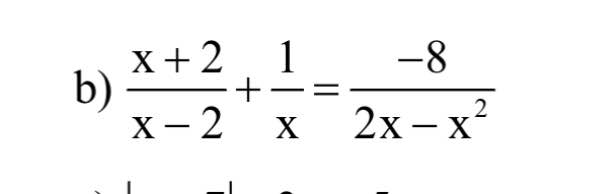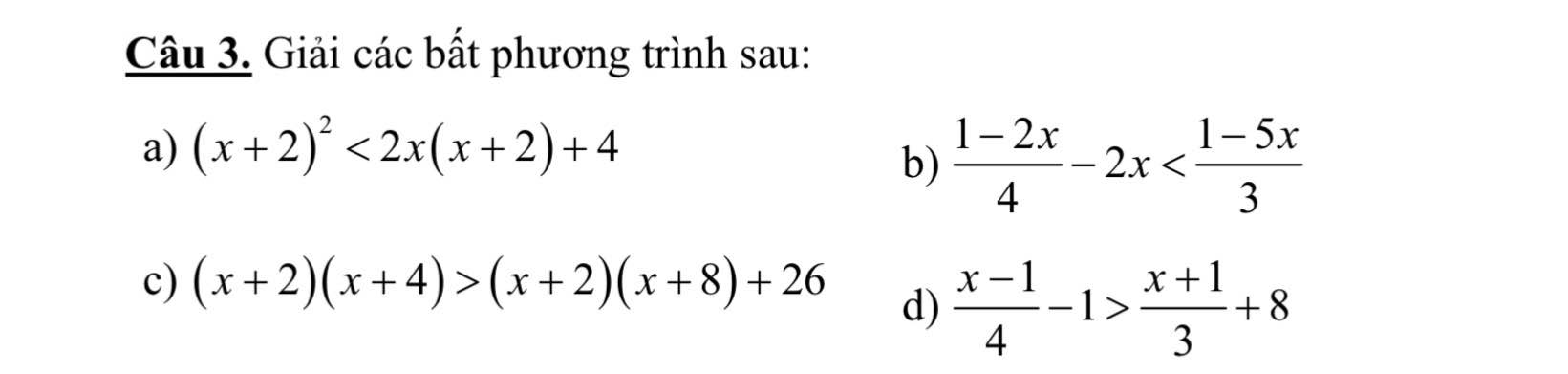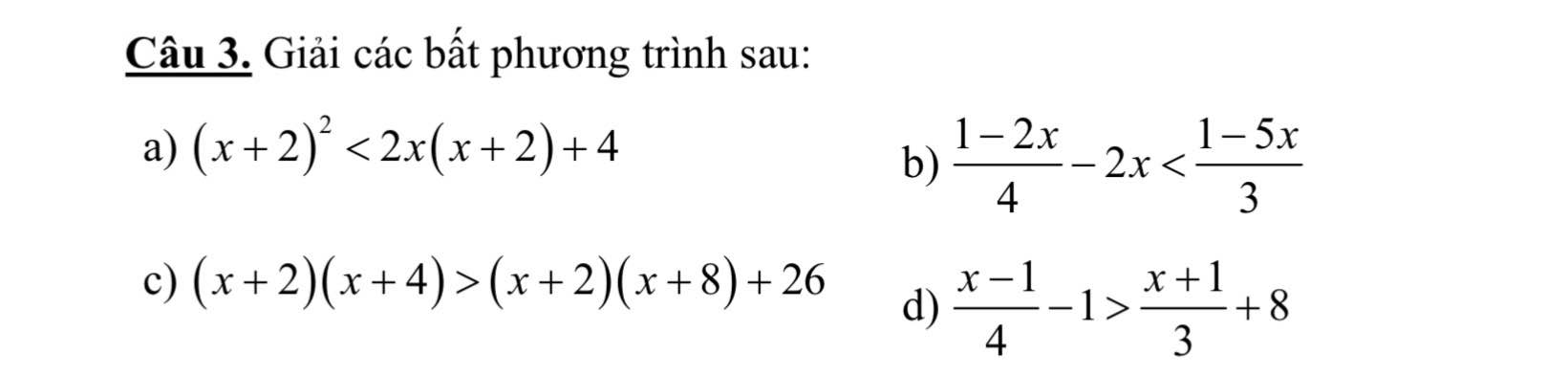Question

Mn giúp tui vs

Answer 1

\(\dfrac{7}{x-1}-\dfrac{1}{3\left(x+1\right)}=\dfrac{x}{x^2-1}\left(x\ne\pm1\right).\\ \Leftrightarrow\dfrac{21x+21-x+1}{x^2-1}=\dfrac{3x}{x^2-1}.\\ \Rightarrow17x=-22.\\ \Leftrightarrow x=\dfrac{-22}{17}\left(TM\right).\)

\(\dfrac{3x}{x-2}-\dfrac{x}{x-5}-\dfrac{2x}{x^2-7x+10}=0\left(x\ne2;5\right).\\ \Leftrightarrow\dfrac{3x}{x-2}-\dfrac{x}{x-5}-\dfrac{2x}{\left(x-5\right)\left(x-2\right)}=0.\\ \Rightarrow3x^2-15x-x^2+2x-2x=0.\\ \Leftrightarrow2x^2-15x=0.\\ \Leftrightarrow x\left(2x-15\right)=0.\Leftrightarrow\left[{}\begin{matrix}x=0.\\x=\dfrac{15}{2}.\end{matrix}\right.\)

(TMĐK).