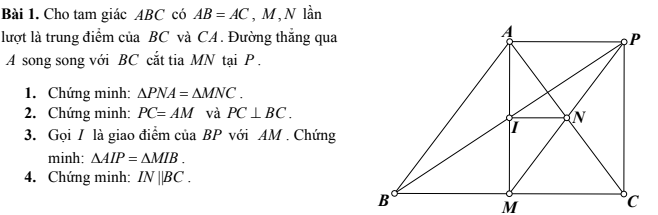
a/ Ta có \(\widehat{B}=\widehat{C}\) => tam giác ABC cân tại A => AB=AC
AM là phân giác góc \(\widehat{A}\)
=> AM là đường cao của tg ABC (trong tg cân phân giác của góc ở đỉnh đồng thời là đường cao và đường trung trực)
\(\Rightarrow MB=MC\)
\(\Rightarrow AM\perp BC\Rightarrow\widehat{AMB}=\widehat{AMC}=90^o\)
b/ Xét tg BMI có
\(\widehat{AIB}=\widehat{AMB}+\widehat{IBM}\) (trong tg góc ngoài bằng tổng hai góc trong không kề với nó)
\(\Rightarrow\widehat{AIB}=90^o+\frac{\widehat{B}}{2}\) mà \(\widehat{B}=\widehat{C}\Rightarrow\widehat{AIB}=90^o+\frac{\widehat{C}}{2}\)
c/ Ta có
MN//AC;\(MB=MC\Rightarrow NA=NB=\frac{AB}{2}\) (Trong tg đường thẳng // với 1 cạnh và đi qua trung điểm 1 cạnh thì đi qua trung điểm cạnh còn lại)
=> MN là đường trung bình của tg ABC \(\Rightarrow MN=\frac{AC}{2}=\frac{AB}{2}\)
\(\Rightarrow MN=NA\) => tg AMN cân tại N \(\Rightarrow\widehat{NAM}=\widehat{NMA}\)
d/ Ta có \(\widehat{AIB}=90^o+\frac{\widehat{C}}{2}\Rightarrow\widehat{B}=\widehat{C}=2\widehat{AIB}-180^o=40^o\)
\(\Rightarrow\widehat{A}=180^o-\left(\widehat{B}+\widehat{C}\right)=180^o-80^o=100^o\)