Chọn D
Viết phương trình mặt phẳng (ABC). Ta có

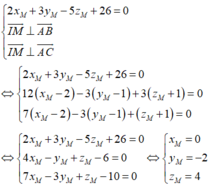
Chọn D
Viết phương trình mặt phẳng (ABC). Ta có

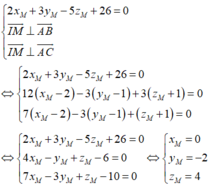
Trong không gian với hệ tọa độ Oxyz cho điểm A(2;2;-3) mặt phẳng (P): 2x-3y+z+19=0. Phương trình mặt cầu tâm A tiếp xúc với mặt phẳng (P) là
![]()
![]()
![]()
![]()
Trong không gian Oxyz, cho mặt cầu S : x 2 + y 2 + z 2 - 4 x + 6 y - 3 = 0 và điểm A(2;1;-2). Đường thẳng d đi qua A, tiếp xúc với (S) tại M luôn nằm trên mặt nón (N) cố định. Tọa độ tâm đường tròn đáy của (N) là H(a;b;c). Giá trị 3a-2b+c bằng
A. 8.
B. 4.
C. 2.
D. 6 5 .
Trong không gian Oxyz, cho mặt phẳng ( P ) : 2 x + 3 y + z – 11 = 0 . Mặt cầu (S) có tâm I(1;-2;1) và tiếp xúc với mặt phẳng (P) tại đim H, khi đó H có tọa độ là:
A. H(-3;-1;-2)
B. H(-1;-5;0)
C. H(1;5;0)
D. H(3;1;2)
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng 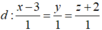 và điểm M(2; -1; 0). Gọi (S) là mặt cầu có tâm I thuộc đường thẳng d và tiếp xúc với mp (Oxy) tại điểm M. Hỏi có bao nhiêu mặt cầu thỏa mãn?
và điểm M(2; -1; 0). Gọi (S) là mặt cầu có tâm I thuộc đường thẳng d và tiếp xúc với mp (Oxy) tại điểm M. Hỏi có bao nhiêu mặt cầu thỏa mãn?
A. 2.
B. 1.
C. 0.
D. Vô số.
Trong không gian với hệ tọa độ Oxyz cho mặt phẳng (P): x-y+2z-6=0 và điểm M(1;-1;2). Phương trình mặt cầu tâm nằm trên trục Ox và tiếp xúc với mặt phẳng (P) tại điểm M là
![]()
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d : x 2 = y - 3 1 = z - 2 1 và hai mặt phẳng
(P): x-2y+2z=0. (Q): x-2y+3z-5=0. Mặt cầu (S) có tâm I là giao điểm của đường thẳng d và mặt phẳng (P). Mặt phẳng (Q) tiếp xúc với mặt cầu (S). Viết phương trình của mặt cầu (S).
![]()
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oxyz cho hai mặt cầu ( S 1 ) , ( S 2 ) lần lượt có phương trình là x 2 + y 2 + z 2 - 2 x - 2 y - 2 z - 22 = 0 , x 2 + y 2 + z 2 - 6 x + 4 y + 2 z + 5 = 0 . Xét các mặt phẳng (P) thay đổi nhưng luôn tiếp xúc với cả hai mặt cầu đã cho. Gọi M(a;b;c) là điểm mà tất cả các mp(P) đi qua. Tính tổng S=a+b+c
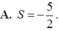
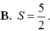
![]()
![]()
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d : x - 3 1 = y 1 = z + 2 1 và điểm M (2; -1; 0). Gọi (S) là mặt cầu có tâm I thuộc đường thẳng d và tiếp xúc với mp (Oxy) tại điểm M. Hỏi có bao nhiêu mặt cầu thỏa mãn?
A. 2.
B. 1
C. 0.
D. Vô số.
Trong không gian với hệ tọa độ Oxyz cho A (1; 2; -3), B (3/2; 3/2; -1/2), C (1; 1; 4), D (5; 3; 0). Gọi (S1) là mặt cầu tâm A bán kính bằng 3, (S2) là mặt cầu tâm B bán kính bằng 3/2. Có bao nhiêu mặt phẳng tiếp xúc với 2 mặt cầu (S1), (S2) đồng thời song song với đường thẳng đi qua 2 điểm C, D.
A. 1
B. 2
C. 4
D. Vô số.