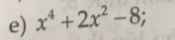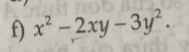e)
\(x^4+2x^2-8\)
\(=x^4+4x^2-2x^2-8\)
\(=\left(x^4-2x^2\right)+\left(4x^2-8\right)\)
\(=x^2\left(x^2-2\right)+4\left(x^2-2\right)\)
\(=\left(x^2+4\right).\left(x^2-2\right)\)
f)
\(x^2-2xy-3y^2\)
\(=x^2-xy+3xy-3y^2\)
\(=\left(x^2-xy\right)+\left(3xy-3y^2\right)\)
\(=x\left(x-y\right)+3y\left(x-y\right)\)
\(=\left(x+3y\right).\left(x-y\right)\)
e, <=> \(x^4+4x^2-2x^2-8\)
<=> \(\left(x^2-2\right)\left(x^2-4\right)\) <=> \(\left(x^2-2\right)\left(x+2\right)\left(x-2\right)\)
f, <=> \(x^2+xy-3xy-3y^2\) <=> \(\left(x-3y\right)\left(x+y\right)\)
học tốt !
e) X^2 + 2x^2 -8
=x^2 +4x^2 -2x^2 -8
= ( x^2 -2)(x^2 +4)
f) x^2 - 2xy - 3y^2
= x^2 -2xy + y^2 -4y^2
= ( x-3y)(x+y)