Đáp án B
Phương trình chính tắc của elip có dạng:
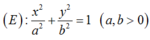
Do một cạnh của hình chữ nhật cơ sở thuộc đường thẳng x-2 = 0 nên có a= 2.
Mặt khác độ dài đường chéo là 6 nên a2 + b2= 62 nên b2= 36- 4= 32
=> ![]()
Vậy (E) cần tìm là:
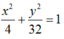
Đáp án B
Phương trình chính tắc của elip có dạng:
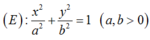
Do một cạnh của hình chữ nhật cơ sở thuộc đường thẳng x-2 = 0 nên có a= 2.
Mặt khác độ dài đường chéo là 6 nên a2 + b2= 62 nên b2= 36- 4= 32
=> ![]()
Vậy (E) cần tìm là:
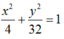
Trong mặt phẳng với hệ trục tọa đô, cho hai đường thẳng x+ y-1= 0 và 3x –y+ 5= 0. Hãy tìm diện tích hình bình hành có hai cạnh nằm trên hai đường thẳng đã cho, một đỉnh là giao điểm của hai đường thẳng đó và giao điểm của hai đường chéo là I(3;3).
A. 74
B. 55
C. 54
D. 65.
trong mặt phẳng toạ độOxy ,cho hinh̀ chữ nhật ABCD có phương trinh̀ đường thẳng AB :x̣-2y+1=0 và đương̀ chéo BD:x-7y+14=0.
a.tim̀ toạ độ điểm B.
b.viết phương trinh̀ tổng quát cuả đương̀ thăng̉ BC.
c.viết phương trinh̀đương̀ troǹ tâm B có bań kính BI biết I(-1/5;-3/5)
Một cung lượng giác trên đường tròn định hướng có độ dài bằng hai lần bán kính. Số đo theo rađian của cung đó là
A. 1 hoặc -1
B. 2 hoặc -2
C. 4 hoặc -4
D. 1/2 hoặc -1/2
cho tam giác ABC có A(-2;3) vá hai đường trung tuyến qua điểm B và điểm C lần lượt là 2x-y+1= 0 , x+y-4=0. Hãy viết phương trình ba đường thẳng chứa ba cạnh của tam giác.
Trong mặt phẳng với hệ trục tọa độ Oxy; tam giác ABC có đỉnh A( 2;-3) ; B( 3;-2) và diện tích tam giác ABC bằng 3/2. Biết trọng tâm G của tam giác ABC thuộc đường thẳng d: 3x- y- 8= 0. Tìm tọa độ điểm C.
A. C( -1; 1) và C( 2 ; -3)
B. C( 1;-1)và C( -2 ; 10)
C. ( 1;-1) và C(2 ; -6)
D. C( 1;1) và C( 2 ; -3)
Trong mặt phẳng với hệ trục tọa độ Oxy cho elip (E) có phương trình chính tắc \(\dfrac{x^2}{25}+\dfrac{y^2}{9}=1\). Độ dài trục lớn của elip (E) là:
A. 10 B. 25 C. 9 D. 6
Cho tam giác ABC, có A(2;1), B(6,15), D(4,9) Viết phương trình tổng quát của đường thẳng AB. Đường cao AH và đường phân giác của góc A
trong mặt phẳng oxy, cho đường tròn (C):\(x^2+y^2-8x+6y+ 21=0\) và đường thẳng d: \(x+ y-1=0\)
Hai tiếp tuyến của đường tròn C tại A,B vuông góc với nhau tại điểm N. Biết N thuộc đường thẳng d. Tìm toạ độ điểm N
Cho elíp E : x 2 16 + y 2 9 = 1 và đường thẳng d: 3x+ 4y -12= 0. Số giao điểm của đường thẳng d và elip (E) là:
A. 0
B.1
C. 2
D. 3