Các câu hỏi tương tự
Cho lăng trụ tam giác đều ABCA’B’C’ có AA
a
2
,
∆
ABC đều cạnh a. Tính diện tích S của
∆
ABC. A. S
a
2
3
4
B. S
a
3
3
2
C. S...
Đọc tiếp
Cho lăng trụ tam giác đều ABCA’B’C’ có AA' = a 2 , ∆ ABC đều cạnh a. Tính diện tích S của ∆ A'BC.
A. S = a 2 3 4
B. S = a 3 3 2
C. S = a 2 2 2
D. S = a 2 2
Cho hình lăng trụ tam giác đều có cạnh đáy và cạnh bên đều bằng a. Gọi S là diện tích xung quanh của hình lăng trụ trên. Tính S. A.
S
3
a
2
4
B. S 5a2 C.
S
3
a
2
2
D. S 3a2.
Đọc tiếp
Cho hình lăng trụ tam giác đều có cạnh đáy và cạnh bên đều bằng a. Gọi S là diện tích xung quanh của hình lăng trụ trên. Tính S.
A. S = 3 a 2 4
B. S = 5a2
C. S = 3 a 2 2
D. S = 3a2.
Cho lăng trụ tam giác đều ABC.ABC có cạnh đáy bằng a, cạnh bên bằng
a
3
. Diện tích toàn phần S của lăng trụ là: A.
S
3
a
2
3
B.
S
7
a
2
3
2
C.
S
3...
Đọc tiếp
Cho lăng trụ tam giác đều ABC.A'B'C' có cạnh đáy bằng a, cạnh bên bằng a 3 . Diện tích toàn phần S của lăng trụ là:
A. S = 3 a 2 3
B. S = 7 a 2 3 2
C. S = 3 a 2 3 2
D. S = 13 a 2 3 4
Cho lăng trụ đều ABC.EFH có tất cả các cạnh bằng a. Gọi S là điểm đối xứng của A qua BH. Thể tích khối đa diện ABCSFH bằng
Đọc tiếp
Cho lăng trụ đều ABC.EFH có tất cả các cạnh bằng a. Gọi S là điểm đối xứng của A qua BH. Thể tích khối đa diện ABCSFH bằng
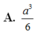
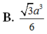
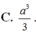
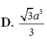
Cho lăng trụ đều
A
B
C
.
A
B
C
có tất cả các cạnh bằng a. Gọi S là điểm đối xứng của A qua
B
C
. Thể tích khối đa diện
A
B
C
S
B
C
là:
Đọc tiếp
Cho lăng trụ đều A B C . A ' B ' C ' có tất cả các cạnh bằng a. Gọi S là điểm đối xứng của A qua B C ' . Thể tích khối đa diện A B C S B ' C ' là:
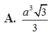
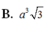
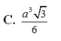
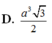
Cho hình lăng trụ đều có độ dài cạnh đáy bằng a. Chiều cao của hình lăng trụ bằng h, diện tích một mặt đáy bằng S. Tổng khoảng cách từ một điểm trong của hình lăng trụ đến tất cả các mặt của hình lăng trụ bằng
Đọc tiếp
Cho hình lăng trụ đều có độ dài cạnh đáy bằng a. Chiều cao của hình lăng trụ bằng h, diện tích một mặt đáy bằng S. Tổng khoảng cách từ một điểm trong của hình lăng trụ đến tất cả các mặt của hình lăng trụ bằng
![]()
![]()
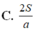
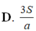
Cho hình lăng trụ tam giác đều ABC.ABC có tất cả các cạnh đều bằng a. Tính diện tích của mặt cầu ngoại tiếp hình lăng trụ theo a.
Đọc tiếp
Cho hình lăng trụ tam giác đều ABC.AB'C' có tất cả các cạnh đều bằng a. Tính diện tích của mặt cầu ngoại tiếp hình lăng trụ theo a.
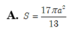
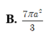
![]()
![]()
Cho hình lăng trụ tam giác đều ABC.ABC có tất cả các cạnh đều bằng a. Tính diện tích của mặt cầu ngoại tiếp hình lăng trụ theo a.
Đọc tiếp
Cho hình lăng trụ tam giác đều ABC.A'B'C' có tất cả các cạnh đều bằng a. Tính diện tích của mặt cầu ngoại tiếp hình lăng trụ theo a.
![]()
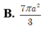
![]()
![]()
Cho lăng trụ ABCA’B’C’ có đáy ABC là tam giác đều cạnh 2
α
. Hình chiếu vuông góc của A’ trên (ABC) là trung điểm H của BC, góc giữa AA’ và (ABC) bằng 450. Thể tích của khối lăng trụ ABCA’B’C’ bằng
Đọc tiếp
Cho lăng trụ ABCA’B’C’ có đáy ABC là tam giác đều cạnh 2 α . Hình chiếu vuông góc của A’ trên (ABC) là trung điểm H của BC, góc giữa AA’ và (ABC) bằng 450. Thể tích của khối lăng trụ ABCA’B’C’ bằng
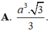
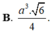
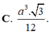
![]()



