Các câu hỏi tương tự
Lớp 5A có 35 học sinh làm bài kiểm tra Toán. Đề bài gồm có 3 bài toán: bài toán 1, bài toán 2, bài toán 3. Sau khi kiểm tra cô giáo tổng hợp được kết quả như sau: có 20 em giải được bài toán thứ 1, có 14 em giải được bài toán thứ 2, có 10 em giải được bài toán thứ 3, 5 em giải được bài toán thứ 2 và thứ 3 , có 2 em giải được bài toán thứ 1 và thứ 2, có sáu em làm được bài toán thứ 1 và thứ 3, chỉ có một em đạt được điểm 10 vì đã giải được cả 3 bài toán. Hỏi lớp học đó có bao nhiêu học sinh không...
Đọc tiếp
Lớp 5A có 35 học sinh làm bài kiểm tra Toán. Đề bài gồm có 3 bài toán: bài toán 1, bài toán 2, bài toán 3. Sau khi kiểm tra cô giáo tổng hợp được kết quả như sau: có 20 em giải được bài toán thứ 1, có 14 em giải được bài toán thứ 2, có 10 em giải được bài toán thứ 3, 5 em giải được bài toán thứ 2 và thứ 3 , có 2 em giải được bài toán thứ 1 và thứ 2, có sáu em làm được bài toán thứ 1 và thứ 3, chỉ có một em đạt được điểm 10 vì đã giải được cả 3 bài toán. Hỏi lớp học đó có bao nhiêu học sinh không giải được bài toán nào?
Một lớp học có 40 học sinh, biết rằng các bạn đều có khả năng được chọn như nhau, số cách chọn ra ba bạn để phân công làm tổ trưởng tổ 1, tổ 2 và tổ 3 là
A
.
A
40
3
B
.
C
40
3
C
.
3
!
D
.
3
C
40...
Đọc tiếp
Một lớp học có 40 học sinh, biết rằng các bạn đều có khả năng được chọn như nhau, số cách chọn ra ba bạn để phân công làm tổ trưởng tổ 1, tổ 2 và tổ 3 là
A . A 40 3
B . C 40 3
C . 3 !
D . 3 C 40 3
Có hai chiếc hộp chứa các viên bi.Hộp 1 có 3 bi đỏ và 2 bi trắng, hộp 2 có 1 bi đỏ và 2 bi trắng Chọn ngẫu nhiên từ mỗi hộp ra 1 viên bi. Tính khả năng để chọn được 2 viên bi khác nhau
Một đề kiểm tra Toán Đại số và Giải tích chương 2 của khối 11 có 20 câu trắc nghiệm. Mỗi câu có 4 phương án lựa chọn, trong đó chỉ có 1 đáp án đúng. Mỗi câu trả lời đúng được 0,5 điểm và mỗi câu trả lời sai không được điểm nào. Một học sinh không học bài nên tích ngẫu nhiên câu trả lời. Tính xác suất để học sinh nhận được 6 điểm (kết quả làm tròn đến 4 chữ số sau dấu phẩy thập phân). A. 0,7873 B.
1
4
C. 0,0609 D. 0,0008
Đọc tiếp
Một đề kiểm tra Toán Đại số và Giải tích chương 2 của khối 11 có 20 câu trắc nghiệm. Mỗi câu có 4 phương án lựa chọn, trong đó chỉ có 1 đáp án đúng. Mỗi câu trả lời đúng được 0,5 điểm và mỗi câu trả lời sai không được điểm nào. Một học sinh không học bài nên tích ngẫu nhiên câu trả lời. Tính xác suất để học sinh nhận được 6 điểm (kết quả làm tròn đến 4 chữ số sau dấu phẩy thập phân).
A. 0,7873
B. 1 4
C. 0,0609
D. 0,0008
Bạn Nam làm bài thi thử THPT Quốc gia môn Toán có 50 câu, mỗi câu có 4 đáp án khác nhau, mỗi câu đúng được 0,2 điểm, mỗi câu làm sai hoặc không làm không được điểm cũng không bị trừ điểm. Bạn Nam đã làm đúng được 40 câu còn 10 câu còn lại bạn chọn ngẫu nhiên mỗi câu một đáp án. Xác suất để bạn Nam được trên điểm gần với số nào nhất trong các số sau? A. 0,53 B. 0,47 C. 0,25 D. 0,99
Đọc tiếp
Bạn Nam làm bài thi thử THPT Quốc gia môn Toán có 50 câu, mỗi câu có 4 đáp án khác nhau, mỗi câu đúng được 0,2 điểm, mỗi câu làm sai hoặc không làm không được điểm cũng không bị trừ điểm. Bạn Nam đã làm đúng được 40 câu còn 10 câu còn lại bạn chọn ngẫu nhiên mỗi câu một đáp án. Xác suất để bạn Nam được trên điểm gần với số nào nhất trong các số sau?
A. 0,53
B. 0,47
C. 0,25
D. 0,99
Người ta sử dụng 5 cuốn sách Toán, 6 cuốn sách Lý, 7 cuốn Hóa (các cuốn sách cùng loại thì giống nhau) để làm phần thưởng cho 9 học sinh, mỗi học sinh được 2 cuốn sách khác loại. Trong số 9 học sịnh có hai bạn an và Bình. Xác suất để hai bạn đó có giải thưởng giống nhau là
Đọc tiếp
Người ta sử dụng 5 cuốn sách Toán, 6 cuốn sách Lý, 7 cuốn Hóa (các cuốn sách cùng loại thì giống nhau) để làm phần thưởng cho 9 học sinh, mỗi học sinh được 2 cuốn sách khác loại. Trong số 9 học sịnh có hai bạn an và Bình. Xác suất để hai bạn đó có giải thưởng giống nhau là
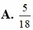
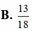
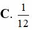
![]()
Nhằm chào mừng ngày thành lập Đoàn TNCS Hồ Chí Minh, Đoàn trường THPT chuyên Lương Thế Vinh đã tổ chức giải bóng đá nam. Có 16 đội đăng kí tham dự trong đó có 3 đội: 10 Toán, 11 Toán, 12 Toán. Ban tổ chức cho bốc thăm ngẫu nhiên để chia đều 16 đội vào 4 bảng để đá vòng loại. Tính xác suất để 3 đội của 3 lớp Toán nằm ở bảng khác nhau.
A
.
53
56
B
.
19
28...
Đọc tiếp
Nhằm chào mừng ngày thành lập Đoàn TNCS Hồ Chí Minh, Đoàn trường THPT chuyên Lương Thế Vinh đã tổ chức giải bóng đá nam. Có 16 đội đăng kí tham dự trong đó có 3 đội: 10 Toán, 11 Toán, 12 Toán. Ban tổ chức cho bốc thăm ngẫu nhiên để chia đều 16 đội vào 4 bảng để đá vòng loại. Tính xác suất để 3 đội của 3 lớp Toán nằm ở bảng khác nhau.
A . 53 56
B . 19 28
C . 16 35
D . 3 56
Có 3 quyển sách toán, 4 quyển sách lý và 5 quyển sách hóa khác nhau được sắp xếp ngẫu nhiên lên một giá sách có 3 ngăn, các quyển sách được sắp dựng đứng thành một hàng dọc vào một trong 3 ngăn ( mỗi ngăn đủ rộng để chứa tất cả các quyển sách). Tính xác suất để không có bất kỳ hai quyển sách toán nào đứng cạnh nhau.
A
.
36
91
B
.
37
91
C...
Đọc tiếp
Có 3 quyển sách toán, 4 quyển sách lý và 5 quyển sách hóa khác nhau được sắp xếp ngẫu nhiên lên một giá sách có 3 ngăn, các quyển sách được sắp dựng đứng thành một hàng dọc vào một trong 3 ngăn ( mỗi ngăn đủ rộng để chứa tất cả các quyển sách). Tính xác suất để không có bất kỳ hai quyển sách toán nào đứng cạnh nhau.
A . 36 91
B . 37 91
C . 54 91
D . 55 91
Ngoài các phương pháp dạy học đã được giới thiệu trong Những vấn đề chung về phương pháp dạy học và giáo dục phát triển phẩm chất, năng lực quý Thầy/Cô còn biết các phương pháp dạy học nào khác để phát triển phẩm chất và năng lực trong môn Toán?






