Các câu hỏi tương tự
Kí hiệu
z
1
,
z
2
là hai nghiệm phức của phương trình
z
2
+
z
+
1
0
Giá trị của biểu thức P...
Đọc tiếp
Kí hiệu z 1 , z 2 là hai nghiệm phức của phương trình z 2 + z + 1 = 0
Giá trị của biểu thức P= z 1 2 + z 2 2 + z 1 z 2 bằng:
A. P=2
B. P=-1
C. P=0
D. P=1
Cho số phức z thỏa mãn
z
≤
2
. Giá trị nhỏ nhất của biểu thức
P
2
z
+
1
+
2
z
-
1
+
z
-
z
¯
-
4
i
bằn...
Đọc tiếp
Cho số phức z thỏa mãn z ≤ 2 . Giá trị nhỏ nhất của biểu thức P = 2 z + 1 + 2 z - 1 + z - z ¯ - 4 i bằng
![]()
![]()
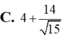
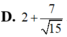
Cho số phức z thỏa điều kiện
z
+
2
z
+
2
i
. Giá trị nhỏ nhất của biểu thức
P
z
-
1...
Đọc tiếp
Cho số phức z thỏa điều kiện z + 2 = z + 2 i .
Giá trị nhỏ nhất của biểu thức P = z - 1 - 2 i + z - 3 - 4 i + z - 5 - 6 i được viết dưới dạng ( a + b 17 ) 2 với a, b là các hữu tỉ.
Giá trị của a + b là
A. 4
B. 2
C. 7
D. 3
Kí hiệu là hai nghiệm phức của phương trình
3
z
2
-
z
+
1
0
.Tính P
z
1
+
z
2
A
.
P
14
3...
Đọc tiếp
Kí hiệu là hai nghiệm phức của phương trình 3 z 2 - z + 1 = 0 .Tính P = z 1 + z 2
A . P = 14 3
B . P = 2 3
C . P = 3 3
D . P = 2 3 3
Cho số phức zx+yi với x, y là các số thực không âm thỏa mãn
z
-
3
z
-
1
+
2
i
1
và biểu thức
P
z
2
-...
Đọc tiếp
Cho số phức z=x+yi với x, y là các số thực không âm thỏa mãn z - 3 z - 1 + 2 i = 1 và biểu thức P = z 2 - z - 2 + i ( z 2 - z - 2 ) z ( 1 - i ) + z ¯ ( 1 + i ) . Giá trị lớn nhất và giá trị nhỏ nhất của P lần lượt là:
A. 0 và -1
B. 3 và -1
C. 3 và 0
D. 2 và 0
Trong tập các số phức, gọi
z
1
,
z
2
là hai nghiệm của phương trình
z
2
-
z
+
2017
4
0
với ...
Đọc tiếp
Trong tập các số phức, gọi z 1 , z 2 là hai nghiệm của phương trình z 2 - z + 2017 4 = 0 với z 2 có thành phần ảo dương. Cho số phức z thỏa mãn z - z 1 = 1 . Giá trị nhỏ nhất của P = z - z 2 là
A. 2016 - 1
B. 2017 - 1 2
C. 2016 - 1 2
D. 2017 - 1
Trong tập các số phức, gọi
z
1
,
z
2
là hai nghiệm của phương trình
z
2
-
z
+
2017
4
0
với
z
2
có thành phần ảo dương. Cho số phức z thỏa mãn
z
-
z...
Đọc tiếp
Trong tập các số phức, gọi z 1 , z 2 là hai nghiệm của phương trình z 2 - z + 2017 4 = 0 với z 2 có thành phần ảo dương. Cho số phức z thỏa mãn z - z 1 = 1 Giá trị nhỏ nhất của P = z - z 2 là
![]()
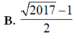
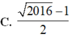
![]()
Cho số phức z thỏa điều kiện
z
+
2
z
+
2
i
. Giá trị nhỏ nhất của biểu thức
P
z
-
1
-
2...
Đọc tiếp
Cho số phức z thỏa điều kiện z + 2 = z + 2 i . Giá trị nhỏ nhất của biểu thức P = z - 1 - 2 i + z - 3 - 4 i + z - 5 - 6 i được viết dưới dạng a + b 17 2 với a, b là các hữu tỉ. Giá trị của a + b là
A. 4.
B. 2.
C. 7.
D. 3.
Cho z và w là các số phức thỏa mãn các điều kiện
z
w
+
1
+
i
w
-
1
0
;
w
+
2
1
. Giá trị nhỏ nhất của biểu thức
T
z
-
1
-
3...
Đọc tiếp
Cho z và w là các số phức thỏa mãn các điều kiện z w + 1 + i w - 1 = 0 ; w + 2 = 1 . Giá trị nhỏ nhất của biểu thức T = z - 1 - 3 i bằng
A. 2 2
B. 4 2
C. 3 2
D. 5 2




