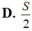Các câu hỏi tương tự
Kí hiệu S(t) là diện tích của hình phẳng giới hạn bởi các đường y2x+1,y0,x1,xt, (t1). Tìm t để S(t) 10
Đọc tiếp
Kí hiệu S(t) là diện tích của hình phẳng giới hạn bởi các đường y=2x+1,y=0,x=1,x=t, (t>1). Tìm t để S(t) = 10
![]()
![]()
![]()
![]()
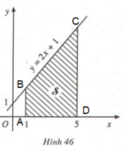
Kí hiệu T là hình thang vuông giới hạn bởi đường thẳng y 2x + 1, trục hoành và hai đường thẳng x 1, x t (1 ≥ t ≥ 5) (H.45).1. Tính diện tích S của hình T khi t 5 (H.46).2. Tính diện tích S(t) của hình T khi x ∈ [1; 5].
Đọc tiếp
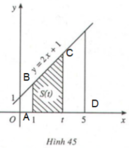
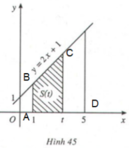
Kí hiệu T là hình thang vuông giới hạn bởi đường thẳng y = 2x + 1, trục hoành và hai đường thẳng x = 1, x = t (1 ≥ t ≥ 5) (H.45).
1. Tính diện tích S của hình T khi t = 5 (H.46).
2. Tính diện tích S(t) của hình T khi x ∈ [1; 5].
Kí hiệu T là hình thang vuông giới hạn bởi đường thẳng y 2x + 1, trục hoành và hai đường thẳng x 1, x t (1 ≥ t ≥ 5) (H.45).1. Tính diện tích S của hình T khi t 5 (H.46).2. Tính diện tích S(t) của hình T khi x ∈ [1; 5].
Đọc tiếp
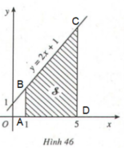
Kí hiệu T là hình thang vuông giới hạn bởi đường thẳng y = 2x + 1, trục hoành và hai đường thẳng x = 1, x = t (1 ≥ t ≥ 5) (H.45).
1. Tính diện tích S của hình T khi t = 5 (H.46).
2. Tính diện tích S(t) của hình T khi x ∈ [1; 5].
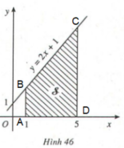
Kí hiệu T là hình thang vuông giới hạn bởi đường thẳng y 2x + 1, trục hoành và hai đường thẳng x 1, x t (1 ≥ t ≥ 5) (H.45).1. Tính diện tích S của hình T khi t 5 (H.46).2. Tính diện tích S(t) của hình T khi x ∈ [1; 5].
Đọc tiếp
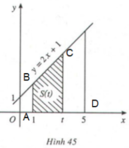
Kí hiệu T là hình thang vuông giới hạn bởi đường thẳng y = 2x + 1, trục hoành và hai đường thẳng x = 1, x = t (1 ≥ t ≥ 5) (H.45).
1. Tính diện tích S của hình T khi t = 5 (H.46).
2. Tính diện tích S(t) của hình T khi x ∈ [1; 5].
Cho hình thang cong (H) giới hạn bởi các đường
y
3
x
,
y
0
,
x
0
,
x
2
. Đường thẳng xt (0t2) chia (H) thành hai phần có diện tích S1 và S2 (như hình vẽ). Tìm t để S13 S2
Đọc tiếp
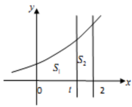
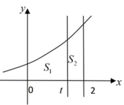
Cho hình thang cong (H) giới hạn bởi các đường y = 3 x , y = 0 , x = 0 , x = 2 . Đường thẳng x=t (0<t<2) chia (H) thành hai phần có diện tích S1 và S2 (như hình vẽ). Tìm t để S1=3 S2
![]()
![]()
![]()
![]()
Cho hình thang cong (H) giới hạn bởi các đường
y
3
x
, y0, x0, x2. Đường thẳng xt chia H thành hai phần có diện tích
S
1
và
S
2
(như hình vẽ). Tìm t để
S
1
3
S
2
Đọc tiếp
Cho hình thang cong (H) giới hạn bởi các đường y = 3 x , y=0, x=0, x=2. Đường thẳng x=t chia H thành hai phần có diện tích S 1 và S 2 (như hình vẽ). Tìm t để S 1 = 3 S 2
![]()
![]()
![]()
![]()
Cắt một vật thể (T) bởi hai mặt phẳng (P) và (Q) vuông góc với trục Ox lần lượt tại xa, xb (ab). Một mặt phẳng tùy ý vuông góc với trục Ox tại điểm x
a
≤
x
≤
b
cắt (T) theo thiết diện có diện tích là S(x). Giả sử S(x) liên tục trên đoạn [a;b]. Thể tích V của phần vật thể (T) giới hạn bởi mặt phẳng (P) và (Q) được cho bởi công thức nào dưới đây? A.
V...
Đọc tiếp
Cắt một vật thể (T) bởi hai mặt phẳng (P) và (Q) vuông góc với trục Ox lần lượt tại x=a, x=b (a<b). Một mặt phẳng tùy ý vuông góc với trục Ox tại điểm x a ≤ x ≤ b cắt (T) theo thiết diện có diện tích là S(x). Giả sử S(x) liên tục trên đoạn [a;b]. Thể tích V của phần vật thể (T) giới hạn bởi mặt phẳng (P) và (Q) được cho bởi công thức nào dưới đây?
A. V = ∫ a b S x d x
B. V = π ∫ a b S x d x
C. V = π 2 ∫ a b S x d x
D. V = π ∫ a b S 2 x d x
Cắt một vật thể (T) bởi hai mặt phẳng (P) và (Q) vuông góc với trục Ox lần lượt tại xa; xb. Một mặt phẳng tùy ý vuông góc với trục Ox tại điểm x cắt (T) theo thiết diện có diện tích là S(x). Giả sử S(x) liên tục trên đoạn [a;b]. Thể tích V của phần vật thể (T) giới hạn bởi mặt phẳng (P) và (Q) được cho bởi công thức nào dưới đây?
Đọc tiếp
Cắt một vật thể (T) bởi hai mặt phẳng (P) và (Q) vuông góc với trục Ox lần lượt tại x=a; x=b. Một mặt phẳng tùy ý vuông góc với trục Ox tại điểm x cắt (T) theo thiết diện có diện tích là S(x). Giả sử S(x) liên tục trên đoạn [a;b]. Thể tích V của phần vật thể (T) giới hạn bởi mặt phẳng (P) và (Q) được cho bởi công thức nào dưới đây?
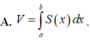
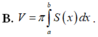
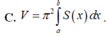
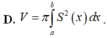
Biết diện tích hình phẳng giới hạn bởi đường cong yf(x), y0, x2a bằng S. Diện tích hình phẳng giới hạn bởi đường cong yf(2x), trục hoành Ox và hai đường thẳng x0, xa bằng:
Đọc tiếp
Biết diện tích hình phẳng giới hạn bởi đường cong y=f(x), y=0, x=2a bằng S. Diện tích hình phẳng giới hạn bởi đường cong y=f(2x), trục hoành Ox và hai đường thẳng x=0, x=a bằng:
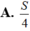
![]()
![]()