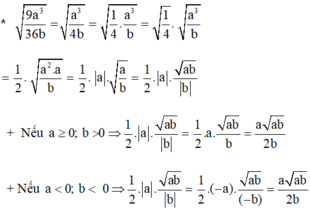
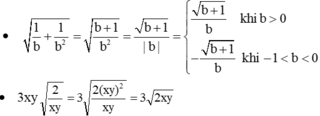
(do xy > 0 (gt) nên đưa thừa số xy vào trong căn để khử mẫu)

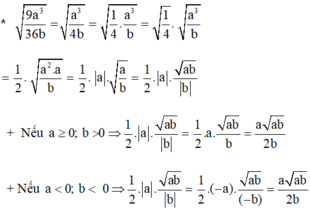
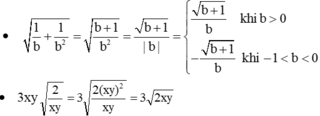
(do xy > 0 (gt) nên đưa thừa số xy vào trong căn để khử mẫu)
Khử mẫu của biểu thức lấy căn
1)√(a/b^2+a/b^4)
2)√a/4 với a>=0
3)√2a/8b^3 với a/b>=0
4)√3/27a^2 với a>0
Khử mẫu của biểu thức lấy căn
1)√(a/b^2+a/b^4)
2)√a/4 với a>=0
3)√2a/8b^3 với a/b>=0
4)√3/27a^2 với a>0
1, x,y,z>=0 ; x+y+z =< 1. cmr: căn(x^2+1/y^2) + căn(y^2+1/z^2) + căn(x^2+1/z^2) >= căn82
2, a,b,c > 0. cm 1/a + 4/b + 9/c >= 36/(a+b+c)
1) Với giá trị nào của x ta có \(x\sqrt{3}=-\sqrt{3x^2}\)
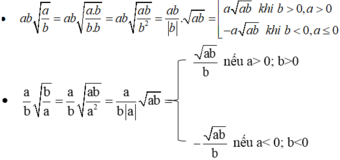
2) Đưa thừa số vào trong dấu căn của biểu thức \(ab^2\sqrt{a}\) với a > 0 ta được :
3) Khử mẫu của biểu thức \(a\sqrt{\dfrac{b}{a}}\) (với a>0) ta được :
Khử mẫu của bthuc lấy căn
a)√3/2a^2
b)√1/600
√11/540
√3/50
√5/98
c)√(1-√3)^2/27
d)√2/3
e)√x^2/5
f) √3/x
g)√x^2- x^2/7
h)ab√a/b
i)a/b√a/b
√1/b +1/b^2
√9a^3/36b
3ab√2/ab
1. x, y, z >=0.
Chứng minh rằng: 4(xy+yz+xz)<=Căn((x+y)(y+z)(x+z))(căn(x+y)+căn(y+z)+căn(x+z)).
2. Cho a, b, c>0 thỏa 1/a+1/b+1/c=3.
Tìm GTLN của P=1/căn(a2-ab+b2)+1/căn(b2-bc+c2)+1/căn(c2-ca+a2)
Khử mẫu của biểu thức lấy căn
a ) 4 5 ; b ) 3 125 c ) 3 2 a 2 v ớ i a > 0
Cho 2 biểu thức
A=(√x / √x-1 - 1/x-√x) : √x+1 / √x+2
B=√x /√x-3
x>0 ; x khác 1;x khác 9
a) tính giá trị biểu thức B khi x=36
b) tìm x để B<1/2
c) rút gọn A
d) tin giá trị x nguyên nhỏ nhất để P=A. B nguyên
cho biểu thức A = (2 căn x +x chia x căn x -1 -1 chia căn x - 1 ) chia ( căn x + 2 chia x + căn x +1 )
a) tìm điều kiện xác định của biểu thức A
b) rút gọn biểu thức A
c) tính giá trị A khi x = 9-4 căn 5
d) tìm giá trị lớn nhất của A
Cho a, b là các số thực dương thỏa mãn a + b = 1. Tìm giá trị nhỏ nhất của biểu thức P = a^2 + b^2 + 1/a + 1/b
Giải phương trình căn(x-1) + căn (3-x) =x^2-4x+6