Các câu hỏi tương tự
Cho khối nón cụt có R, r lần lượt là bán kính hai đáy và h3 là chiều cao. Biết thể tích khối nón cụt là
V
π
tìm giá trị lớn nhất của biểu thức PR+2r A.
2
3
B. 3. C.
3
3
D. 2.
Đọc tiếp
Cho khối nón cụt có R, r lần lượt là bán kính hai đáy và h=3 là chiều cao. Biết thể tích khối nón cụt là V = π tìm giá trị lớn nhất của biểu thức P=R+2r
A. 2 3
B. 3.
C. 3 3
D. 2.
Cho hình nón (N) có bán kính đáy bằng 6 và diện tích xung quanh bằng
60
π
.Tính thể tích V của khối nón (N). A.V
288
π
B. V
96
π
C. V
432
6
π
D. V
144
6
π
Đọc tiếp
Cho hình nón (N) có bán kính đáy bằng 6 và diện tích xung quanh bằng 60 π .Tính thể tích V của khối nón (N).
A.V = 288 π
B. V = 96 π
C. V = 432 6 π
D. V = 144 6 π
Cho hình nón có bán kính đường tròn đáy là 6cm và diện tích hình tròn đáy bằng
3
5
diện tích xung quanh của hình nón. Tính thể tích V khối nón
Đọc tiếp
Cho hình nón có bán kính đường tròn đáy là 6cm và diện tích hình tròn đáy bằng 3 5 diện tích xung quanh của hình nón. Tính thể tích V khối nón
![]()
![]()
![]()
![]()
Cho hình nón có thiết diện qua trục là tam giác đều và có diện tích xung quanh bằng 8
π
Tính chiều cao của hình nón này.
Đọc tiếp
Cho hình nón có thiết diện qua trục là tam giác đều và có diện tích xung quanh bằng 8 π Tính chiều cao của hình nón này.
![]()
![]()
![]()
![]()
Gọi r, h, l lần lượt là bán kính đáy, chiều cao và đường sinh của hình nón (N).
S
x
q
,
S
t
p
,
V
lần lượt là diện tích xung quanh, diện tích toàn phần của hình nón và thể tích của khối nón. Chọn phát biểu sai
A
.
V
1...
Đọc tiếp
Gọi r, h, l lần lượt là bán kính đáy, chiều cao và đường sinh của hình nón (N). S x q , S t p , V lần lượt là diện tích xung quanh, diện tích toàn phần của hình nón và thể tích của khối nón. Chọn phát biểu sai
A . V = 1 3 πrh
B . l 2 = h 2 + r 2
C . S t p = πr ( 1 + r )
D . S x q = πrl
Một khối nón có diện tích toàn phần bằng
10
π
và diện tích xung quanh bằng
6
π
. Tính thể tích V của khối nón đó.
Đọc tiếp
Một khối nón có diện tích toàn phần bằng 10 π và diện tích xung quanh bằng 6 π . Tính thể tích V của khối nón đó.
![]()
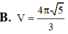
![]()
![]()
Một khối trụ (N) có diện tích xung quanh bằng
4
π
3
và chiều cao là một số nguyên ngoại tiếp một khối nón (N) có đường sinh bằng
7
. Tính thể tích V phần không gian bên ngoài khối nón và bên trong khối trụ.
Đọc tiếp
Một khối trụ (N) có diện tích xung quanh bằng 4 π 3 và chiều cao là một số nguyên ngoại tiếp một khối nón (N') có đường sinh bằng 7 . Tính thể tích V phần không gian bên ngoài khối nón và bên trong khối trụ.
![]()
![]()
![]()
![]()
Cho khối trụ có chiều cao h 3 và diện tích toàn phần bằng 20
π
. Khi đó chu vi đáy của khối trụ là
Đọc tiếp
Cho khối trụ có chiều cao h = 3 và diện tích toàn phần bằng 20 π . Khi đó chu vi đáy của khối trụ là
![]()
![]()
![]()
![]()
Cho hình nón có góc ở đỉnh bằng
60
0
, diện tích xung quanh bằng
6
πa
2
. Tính theo a thể tích V của khối nón đã cho A.
V
3
πa
3
2
4
B.
V
...
Đọc tiếp
Cho hình nón có góc ở đỉnh bằng 60 0 , diện tích xung quanh bằng 6 πa 2 . Tính theo a thể tích V của khối nón đã cho
A. V = 3 πa 3 2 4
B. V = πa 3
C. V = πa 3 2 4
D. V = 3 πa 3




