Các câu hỏi tương tự
Chứng minh rằng trong không gian 3 chiều chỉ có đúng 5 khối đa diện đều: Tứ diện đều (3 mặt tam giác), Lập phương (3 mặt vuông), Bát diện đều (8 mặt tam giác), Thập nhị diện đều (12 mặt ngũ giác) và Nhị thập diện đều (20 mặt tam giác)Mọi người giúp mình giải câu này với ạ :)
Đọc tiếp
Chứng minh rằng trong không gian 3 chiều chỉ có đúng 5 khối đa diện đều: Tứ diện đều (3 mặt tam giác), Lập phương (3 mặt vuông), Bát diện đều (8 mặt tam giác), Thập nhị diện đều (12 mặt ngũ giác) và Nhị thập diện đều (20 mặt tam giác)

Mọi người giúp mình giải câu này với ạ :)
Khối đa diện đều nào sau đây có mặt không phải là tam giác đều?
A. Tám mặt đều
B. Tứ diện đều
C. Mười hai mặt đều
D. Hai mươi mặt đều
Khối đa diện đều nào sau đây có mặt không phải là tam giác đều?
A. Mười hai mặt đều
B. Hai mươi mặt đều
C. Tám mặt đều
D. Tứ diện đều
Cho hình thập nhị diện đều (tham khảo hình vẽ bên). Côsin của góc tạo bởi hai mặt phẳng có chung một cạnh của thập nhị diện đều bằng A.
5
-
1
2
B.
5
-
1
4
C.
1...
Đọc tiếp
Cho hình thập nhị diện đều (tham khảo hình vẽ bên). Côsin của góc tạo bởi hai mặt phẳng có chung một cạnh của thập nhị diện đều bằng
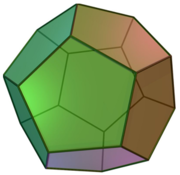
A. 5 - 1 2
B. 5 - 1 4
C. 1 5
D. 1 2
Khối đa diện nào sau đây có các mặt không phải là tam giác đều?
A. Bát diện đều
B. Nhị thập diện đều
C. Tứ diện đều
D. Thập nhị diện đều
Cho khối lập phương ABCD.ABCD. Cắt khối lập phương bởi các mặt phẳng (ABD) và (CBD) ta được ba khối đa diện. Xét các mệnh đề sau: (I): Ba khối đa diện thu được gồm hai khối chóp tam giác đều và một khối lăng trụ tam giác. (II): Ba khối đa diện thu được gồm hai khối tứ diện và một khối bát diện đều. (III): Trong ba khối đa diện thu được có hai khối đa diện bằng nhau. Số mệnh đề đúng là A. 3. B. 2. C. 0. D. 1.
Đọc tiếp
Cho khối lập phương ABCD.A'B'C'D'. Cắt khối lập phương bởi các mặt phẳng (AB'D') và (C'BD) ta được ba khối đa diện. Xét các mệnh đề sau:
(I): Ba khối đa diện thu được gồm hai khối chóp tam giác đều và một khối lăng trụ tam giác.
(II): Ba khối đa diện thu được gồm hai khối tứ diện và một khối bát diện đều.
(III): Trong ba khối đa diện thu được có hai khối đa diện bằng nhau.
Số mệnh đề đúng là
A. 3.
B. 2.
C. 0.
D. 1.
Hình đa diện đều nào dưới đây có tất cả các mặt không phải là tam giác đều? A. Bát diện đều B. Hình 20 mặt đều C. Hình 12 mặt đều D. Tứ diện đều.
Đọc tiếp
Hình đa diện đều nào dưới đây có tất cả các mặt không phải là tam giác đều?
A. Bát diện đều
B. Hình 20 mặt đều
C. Hình 12 mặt đều
D. Tứ diện đều.
Hình đa diện đều nào dưới đây có tất cả các mặt không là tam giác đều A. Bát giác đều B. Hình 20 mặt đều C. Hình 12 mặt đều D. Tứ diện đều
Đọc tiếp
Hình đa diện đều nào dưới đây có tất cả các mặt không là tam giác đều
A. Bát giác đều
B. Hình 20 mặt đều
C. Hình 12 mặt đều
D. Tứ diện đều
Hình bát diện đều thuộc loại khối đa diện đều nào sau đây? A.
5
;
3
B.
4
;
3
C.
3
;
3
D.
3
;
4
Đọc tiếp
Hình bát diện đều thuộc loại khối đa diện đều nào sau đây?
A. 5 ; 3
B. 4 ; 3
C. 3 ; 3
D. 3 ; 4




