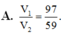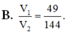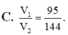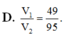Chọn B
Khối đa diện đều loại 4 ; 3 là khối đa diện có các mặt là một tứ giác đều và mỗi đỉnh là đỉnh chung của đúng ba mặt. Vậy khối đa diện đó là khối lập phương.
Do đó, số đỉnh của khối đa diện đều loại 4 ; 3 là 8 đỉnh
Khối đa diện đều loại 4 ; 3 có số đỉnh
A. 4
B. 6
C. 8
D. 10
Hai khối đa diện đều được gọi là đối ngẫu nếu các đỉnh của khối đa diện đều loại này là tâm (đường tròn ngoại tiếp) các mặt của khối đa diện đều loại kia. Hãy tìm khẳng định sai trong các khẳng định sau:
A. Khối tứ diện đều đối ngẫu với chính nó.
B. Hai khối đa diện đều đối ngẫu với nhau luôn có số cạnh bằng nhau.
C. Số mặt của một đa diện đều bằng số cạnh của đa diện đều đối ngẫu với nó.
D. Khối 20 mặt đều đối ngẫu với khối 12 mặt đều.
Cho tứ diện đều ABCD có cạnh bằng a. Gọi M, N lần lượt là trung điểm của các cạnh AB, BC và E là điểm đối xứng với B qua D. Mặt phẳng (MNE) chia khối tứ diện ABCD thành hai khối đa diện, trong đó khối đa diện chứa đỉnh A có thể tích V . Tính V .
A. 7 2 a 3 216
B. 11 2 a 3 216
C. 13 2 a 3 216
D. 2 a 3 18
Cho tứ diện đều ABCD có cạnh bằng a. Gọi M, N lần lượt là trọng tâm của các tam giác ABD, ABC và E là điểm đối xứng với điểm B qua điểm D. Mặt phẳng (MNE) chia khối tứ diện ABCD thành hai khối đa diện, trong đó khối đa diện chứa đỉnh A có thể tích V. Tính V
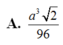
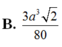
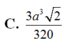
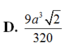
Biết H là đa diện đều loại 3 ; 5 với số đỉnh và số cạnh lần lượt là a và b . Tính a - b
A. a - b = 10
B. a - b = 18
C. a - b = - 8
D. a - b = - 18
Cho khối đa diện đều loại . Tổng các góc phẳng tại 1 đỉnh của khối đa diện bằng
A. 180 °
B. 240 °
C. 324 °
D. 360 °
Khối đa diện 12 mặt đều có số đỉnh và số cạnh lần lượt là
A. 30 và 20
B. 12 và 20
C. 20 và 30
D. 12 và 30
Khối đa diện có mười hai mặt đều có số đỉnh, số cạnh, số mặt lần lượt là:
A. 30, 20, 12
B. 20, 12, 30
C. 12, 30, 20
D. 20, 30, 12
Cho lăng trụ tam giác đều ABC.A’B’C’. Trên A’B, kéo dài lấy điểm M sao cho B'M= 1 2 A'B'. Gọi N, P lần lượt là trung điểm của A’C’ và B’B. Mặt phẳng (MNP) chia khối lăng trụ ABC.A’B’C’ thành hai khối đa diện trong đó khối đa diện chứa đỉnh A’ có thể tích V 1 và khối đa diện chứa đỉnh C’ có thể tích V 2 . Tính V 1 V 2 .
