Các câu hỏi tương tự
Để tính
∫
xln
(
2
+
x
)
.
dx
theo phương pháp tính nguyên hàm từng phần, ta đặt: A.
u
v
d
v
ln
2...
Đọc tiếp
Để tính ∫ xln ( 2 + x ) . dx theo phương pháp tính nguyên hàm từng phần, ta đặt:
A. u = v d v = ln 2 + x d x
B. u = ln 2 + x d v = x d x
C. u = x ln 2 + x d v = d x
D. u = ln 2 + x d v = d x
Để tính
∫
x
ln
(
2
+
x
)
d
x
theo phương pháp tính nguyên hàm từng phần, ta đặt: A.
u
v
d
v
ln
2...
Đọc tiếp
Để tính ∫ x ln ( 2 + x ) d x theo phương pháp tính nguyên hàm từng phần, ta đặt:
A. u = v d v = ln 2 + x d x
B. u = ln 2 + x d v = x d x
C. u = x ln 2 + x d v = d x
D. u = ln 2 + x d v = d x
Cho hàm số f(x) có nguyên hàm là F(x) trên đoạn [1;2], biết F(2) 1 và
∫
1
2
F
(
x
)
d
x
5
. Tính I
∫
1
2
(
x
-
1
)
f
(
x
)
d
x
Đọc tiếp
Cho hàm số f(x) có nguyên hàm là F(x) trên đoạn [1;2], biết F(2) = 1 và ∫ 1 2 F ( x ) d x = 5 . Tính I= ∫ 1 2 ( x - 1 ) f ( x ) d x
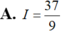
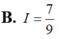
Cho hàm số f(x) có nguyên hàm là F(x) trên đoạn [1;2], biết F(2)1 và
∫
1
2
F
(
x
)
d
x
5
. Tính
I
∫
1
2
(
x
-
1
)
f
(
x
)
d
x
Đọc tiếp
Cho hàm số f(x) có nguyên hàm là F(x) trên đoạn [1;2], biết F(2)=1 và ∫ 1 2 F ( x ) d x = 5 . Tính I = ∫ 1 2 ( x - 1 ) f ( x ) d x
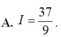
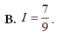
Cho hai hàm số liên tục f(x) và g(x) có nguyên hàm lần lượt là F(x) và G(x) trên [0; 2]. Biết F(0) 0, F(2) 1, G(2) 1 và
∫
0
2
F
(
x
)
g
(
x
)
d
x
3 . Tính tích phân hàm:
∫
0
2
G
(
x
)
f
(
x
)
d
x
A. I 3. B. I 0....
Đọc tiếp
Cho hai hàm số liên tục f(x) và g(x) có nguyên hàm lần lượt là F(x) và G(x) trên [0; 2]. Biết F(0) = 0, F(2) = 1, G(2) = 1 và ∫ 0 2 F ( x ) g ( x ) d x = 3 . Tính tích phân hàm: ∫ 0 2 G ( x ) f ( x ) d x
A. I = 3.
B. I = 0.
C. I = -2.
D. I = -4.
Biết F(x) là một nguyên hàm của f(x) và f(x) xác định trên [a;b]. Khi đó tích phân
∫
a
b
f
(
x
)
d
x
được tính theo công thức nào sau đây?
Đọc tiếp
Biết F(x) là một nguyên hàm của f(x) và f(x) xác định trên [a;b]. Khi đó tích phân ∫ a b f ( x ) d x được tính theo công thức nào sau đây?
Hàm số
f
(
x
)
(
x
-
1
)
e
x
có một nguyên hàm F(x) là kết quả nào sau đây, biết nguyên hàm này bằng 1 khi x 0? A.
F
(
x
)
(
x
-
1
)
e
x
.
B.
F
(
x...
Đọc tiếp
Hàm số f ( x ) = ( x - 1 ) e x có một nguyên hàm F(x) là kết quả nào sau đây, biết nguyên hàm này bằng 1 khi x = 0?
A. F ( x ) = ( x - 1 ) e x .
B. F ( x ) = ( x - 2 ) e x .
C. F ( x ) = ( x + 1 ) e x + 1 .
D. F ( x ) = ( x - 2 ) e x + 3 .
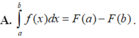
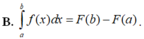
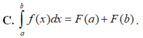
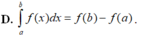
Cho hàm số f(x) xác định và liên tục trên R. Gọi g(x) là một nguyên hàm của y
x
x
+
f
2
(
x
)
hàm số Biết rằng
∫
1
2
g
(
x
)
d
x
1
và 2g(2)-g(1)2 Tích phân
∫...
Đọc tiếp
Cho hàm số f(x) xác định và liên tục trên R. Gọi g(x) là một nguyên hàm của y= x x + f 2 ( x ) hàm số Biết rằng ∫ 1 2 g ( x ) d x = 1 và 2g(2)-g(1)=2 Tích phân
∫ 1 2 x 2 x + f 2 ( x ) d x bằng
A. 1,5
B. 1
C. 3
D. 2
Biết F(x) là một nguyên hàm của hàm số f(x) trên đoạn [a;b] và 2F(a)-12F(b). Tính
I
∫
a
b
f
(
x
)
d
x
. A. I-1. B. I1. C. I
-
1
2
. D. I
1
2
.
Đọc tiếp
Biết F(x) là một nguyên hàm của hàm số f(x) trên đoạn [a;b] và 2F(a)-1=2F(b). Tính I = ∫ a b f ( x ) d x .
A. I=-1.
B. I=1.
C. I= - 1 2 .
D. I= 1 2 .