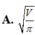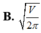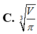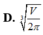Các câu hỏi tương tự
Khi thiết kế vỏ lon sữa hình trụ các nhà thiết kế luôn đặt mục tiêu sao cho chi phí làm vỏ lon là nhỏ nhất. Muốn thể tích khối trụ bằng V mà diện tích toàn phần của hình trụ là nhỏ nhất thì bán kính R của mặt tròn đáy khối trụ bằng?
Đọc tiếp
Khi thiết kế vỏ lon sữa hình trụ các nhà thiết kế luôn đặt mục tiêu sao cho chi phí làm vỏ lon là nhỏ nhất. Muốn thể tích khối trụ bằng V mà diện tích toàn phần của hình trụ là nhỏ nhất thì bán kính R của mặt tròn đáy khối trụ bằng?
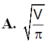
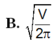
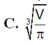
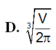
Khi sản xuất vỏ lon sữa bò hình trụ có thể tích là V, các nhà thiết kế luôn đặt mục tiêu sao cho chi phí nguyên liệu làm vỏ lon sữa bò là ít nhất, tức là diện tích toàn phần của hình trụ là nhỏ nhất. Muốn thể tích khối trụ bằng V và diện tích toàn phần hình trụ nhỏ nhất thì bán kính đáy bằng bao nhiêu? A.
r
V
π
2...
Đọc tiếp
Khi sản xuất vỏ lon sữa bò hình trụ có thể tích là V, các nhà thiết kế luôn đặt mục tiêu sao cho chi phí nguyên liệu làm vỏ lon sữa bò là ít nhất, tức là diện tích toàn phần của hình trụ là nhỏ nhất. Muốn thể tích khối trụ bằng V và diện tích toàn phần hình trụ nhỏ nhất thì bán kính đáy bằng bao nhiêu?
A. r = V π 2 3
B. r = V 3
C. r = V 2 π 3
D. r = V 2 3
Khi sản xuất vỏ lon sữa bò hình trụ, các nhà thiết kế đặt mục tiêu sao cho chi phí nguyên liệu làm vỏ hộp ít nhất (diện tích toàn phần của lon nhỏ nhất). Bán kính đáy của vỏ lon là bao nhiêu khi muốn thể tích của lon là 314
c
m
3
. A.
r
314
4
π...
Đọc tiếp
Khi sản xuất vỏ lon sữa bò hình trụ, các nhà thiết kế đặt mục tiêu sao cho chi phí nguyên liệu làm vỏ hộp ít nhất (diện tích toàn phần của lon nhỏ nhất). Bán kính đáy của vỏ lon là bao nhiêu khi muốn thể tích của lon là 314 c m 3 .
A. r = 314 4 π 3 c m
B. r = 942 2 π 3 c m
C. r = 314 2 π 3 c m
D. r = 314 π 3 c m
Một nhà máy sản xuất nước ngọt cần làm các lon dựng dạng hình trụ với thể tích đựng được là V. Biết rằng diện tích toàn phần nhỏ nhất thì tiết kiệm chi phí nhất. Tính bán kính của lon để tiết kiệm chi phí nhất.
Đọc tiếp
Một nhà máy sản xuất nước ngọt cần làm các lon dựng dạng hình trụ với thể tích đựng được là V. Biết rằng diện tích toàn phần nhỏ nhất thì tiết kiệm chi phí nhất. Tính bán kính của lon để tiết kiệm chi phí nhất.
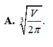
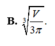
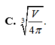
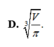
Người ta thiết kế một thùng chứa hình trụ có thể tích V cho trước. Biết rằng đơn giá của vật liệu làm mặt đáy và nắp của thùng bằng nhau và gấp lần đơn giá của vật liệu để làm mặt xung quanh của thùng (chi phí cho mỗi đơn vị diện tích). Gọi chiều cao của thùng là h và bán kính đáy là r. Tính tỉ số
h
r
sao cho chi phí vật liệu sản suất thùng là nhỏ nhất. A.
h
r...
Đọc tiếp
Người ta thiết kế một thùng chứa hình trụ có thể tích V cho trước. Biết rằng đơn giá của vật liệu làm mặt đáy và nắp của thùng bằng nhau và gấp lần đơn giá của vật liệu để làm mặt xung quanh của thùng (chi phí cho mỗi đơn vị diện tích). Gọi chiều cao của thùng là h và bán kính đáy là r. Tính tỉ số h r sao cho chi phí vật liệu sản suất thùng là nhỏ nhất.
A. h r = 2
B. h r = 2
C. h r = 6
D. h r = 3 2
Một nhà máy cần sản suất các hộp hình trụ kín cả hai đầu có thể tích V cho trước. Mối quan hệ giữa bán kính đáy R và chiều cao h của hình trụ để diện tích toàn phần của hình trụ nhỏ nhất là ?
Đọc tiếp
Một nhà máy cần sản suất các hộp hình trụ kín cả hai đầu có thể tích V cho trước. Mối quan hệ giữa bán kính đáy R và chiều cao h của hình trụ để diện tích toàn phần của hình trụ nhỏ nhất là ?
![]()
![]()
![]()
![]()
Cho hình trụ có bán kính đường tròn đáy là R, độ dài đường cao h. Kí hiệu Stp là diện tích toàn phần của hình trụ và V là thể tích khối trụ. Trong các mệnh đề sau, mệnh đề nào đúng? A.
V
1
3
π
R
2
h
B. ...
Đọc tiếp
Cho hình trụ có bán kính đường tròn đáy là R, độ dài đường cao h. Kí hiệu Stp là diện tích toàn phần của hình trụ và V là thể tích khối trụ. Trong các mệnh đề sau, mệnh đề nào đúng?
A. V = 1 3 π R 2 h
B. S t p = π R h
C. S t p = 2 π R h + π R 2 h
D. S t p = 2 π R ( h + R )
Cho hình trụ có bán kính đáy là Ra, mặt phẳng qua trục cắt hình trụ theo một thiết diện có diện tích bằng
8
a
2
. Diện tích xung quanh của hình trụ và thể tích khối trụ là:
Đọc tiếp
Cho hình trụ có bán kính đáy là R=a, mặt phẳng qua trục cắt hình trụ theo một thiết diện có diện tích bằng 8 a 2 . Diện tích xung quanh của hình trụ và thể tích khối trụ là:
![]()
![]()
![]()
![]()
Cho mặt cầu (S) có bán kính
R
a
3
. Gọi (T) là hình trụ có hai đường tròn đáy nằm trên (S) và diện tích thiết diện qua trục của hình trụ (T) là lớn nhất. Tính diện tích toàn phần
S
t
p
của (T) A.
S
t
p
9
π
a
2
.
B. ...
Đọc tiếp
Cho mặt cầu (S) có bán kính R = a 3 . Gọi (T) là hình trụ có hai đường tròn đáy nằm trên (S) và diện tích thiết diện qua trục của hình trụ (T) là lớn nhất. Tính diện tích toàn phần S t p của (T)
A. S t p = 9 π a 2 .
B. S t p = 9 π a 2 3 .
C. S t p = 6 π a 2 3 .
D. S t p = 6 π a 2 .